


Next: About this document ...
- Consider
- Determine the exact solution.
- Using Euler's method, write a computer program in any language
other than a matlab to determine an approximate
solution to the equation.
- Using the fourth order Runge-Kutta method, write a computer
program in any language other than matlab to determine an approximate
solution to the equation.
- In addition to submitting your work for the exact solution and
a listing of each program, submit the a figure plotting the exact solution, the solution from
Euler's method and the solution from the fourth order Runge-Kutta
method on the same plot from
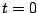 to
to 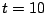 and on a separate plot
for t=0 to t=0.5 for:
and on a separate plot
for t=0 to t=0.5 for:
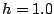
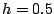
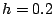
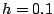
- Consider
- Using Euler's method, write a computer program in any language
other than a matlab to determine an approximate
solution to the equation.
- Using the fourth order Runge-Kutta method, write a computer
program in any language other than matlab to determine an approximate
solution to the equation.
- In addition to submitting your work for the exact solution and
a listing of each program, submit the following a figure plotting the exact solution, the solution from
Euler's method and the solution from the fourth order Runge-Kutta
method on the same plot from t=0 to t=10 for:
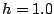
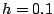
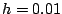
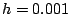
- For the same time steps, submit four plots where the time range
is from
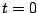 to
to 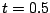 .
.
- Explain what happens between
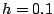 and
and 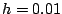 .
.



Next: About this document ...
2003-12-06
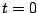 to
to 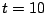 and on a separate plot
for t=0 to t=0.5 for:
and on a separate plot
for t=0 to t=0.5 for:
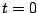 to
to 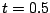 .
.
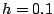 and
and 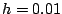 .
.