Save this page!

University of Notre Dame
Aerospace and Mechanical Engineering

AME 437: Control Systems Engineering
Exam 2

B. Goodwine
April 10, 2002

Start time: xxxx
Name: xxxx

It is now 2003 and you still work at Hewlett-Packard ink-jet printer division (like you did for Exam 1). The mechanism which regulates the flow of ink out of an ink-jet cartridge is described by the following block diagram

where Y(s) is the ink flow rate out of the cartridge nozzle and R(s) is the desired ink flow rate.
1. Your boss suggests using proportional control, i.e., D(s) = K to control the flow rate. Using a root locus plot, determine the approximate maximum value for K for which the closed loop system is stable.
  Enter the value you determined here: K = . (5 points)
2. If D(s) = K and K = 10, by plotting the Bode plot for the system, determine the approximate steady state error to different types of inputs:
  1. For a step input, e_ss = . (5 points)
  2. Print and submit a Matlab plot using the step() command verifying your answer for the step input steady state error. (5 points)
  3. For a ramp input, e_ss = . (10 points)
3. Your boss has no faith in the the idiots in the electronics design division and is concerned that there will be a time delay of up to 0.1 second when the electronic circuitry does the necessary computations for D(s). The block diagram for the delayed system is illustrated as follows:
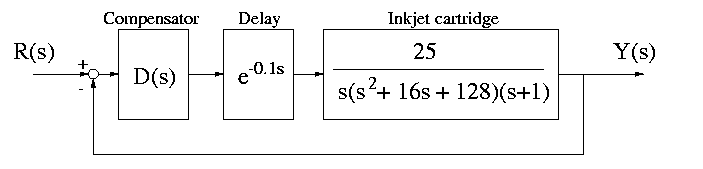
  Using a second order Pade approximation of the time delay, plot a root locus plot of the delayed system using proportional control. Using a root locus plot, determine the approximate maximum value for K for which the closed loop system is stable.
  Enter the value you determined here: K = . (15 points)
  Ignore time delays for the rest of the exam!
4. Referring to the first block diagram, in order to achieve crisp printing characteristics, it is desired that the following specifications be achieved:
  1. rise time: t_r < 0.4 seconds;
  2. maximum overshoot: M_p < 20%
  3. steady state error for a ramp input: e_ss < 1/80.
  4. Where should the dominant closed-loop second order poles be located to achieve the desired transient response?
    Enter the value you determined here: s = (enter something of the form "1 + 2 i"). (5 points)
  5. Referring to your root locus plot from Problem 1a, can this response be obtained using proportional control only?
    Yes or no: . (5 points)
5. Regardless of whether you answered yes or no to the previous question, your boss tells you to design a lead/lag controller to attempt to meet the specifications.
  1. If the zero for the lead controller is placed at s = -3, where (approximately) should the pole for the lead controller be placed to achieve the desired response?
    Enter the value you determined here: p = . (10 points)
  2. What is the value of the gain, K which corresponds to the desired pole locations when the lead compensator is used?
    Enter the value you determined here: K = . (5 points)
  3. Submit a plot of the response of the system to a step input to verify the properties of the lead controller. If there are any discrepancies, attempt to explain them here:
    (5 points)
  4. Now design a lag controller to reduce the steady state error to the desired value of 1/80 to a ramp input. If the pole of the lag controller is placed at s = -0.01, where should the zero be placed?
    Enter the value you determined here: z = . (10 points)
  5. What are the gain and phase margins of the compensated system?
    PM = degrees. (5 points)
    GM = dB. (5 points)
Your clumsy boss had two bode plots and two other plots showing the response of a transfer function to sinusoidal inputs. Unfortunately, the plots were mixed up, and now no one can tell which Bode plot goes with which response plot. Here are the plots:

Tell your boss which plots go together, and be sure to explain why.
(15 points: 2 points for guessing the right answer and 13 points for the correct explanation.)

When you are done, hit the "Submit" button. After you hit this button, you will not be able to change any of your answers. All that you are allowed to do is print any computer-generated plots.

Bill Goodwine

Last modified: Tue Apr 9 19:18:59 EST 2002