Exam 2 from Spring 2002

1. It is now 2005 and you are self-employed as an independent contractor. You have recently been hired by the administration of a medium-sized mid-western teaching and research university. Due to recent events, the university has decided to appease the student body by allowing for greater student input into various aspects of the administrative decision-making process; however, the administration does not really want the student input to actually have much effect on the ultimate outcome. You are the second consultant to work on this project. The first one was fired after only a couple days because of discrepancies in his resume from about 25 years ago; however, he did complete two models of the decision-making process.
   1. In the first model, the relationship among what the administration wants, R(s), what the student body wants, W(s) and the amount of freedom allowed by the rules governing student life, Y(s), is illustrated by the following block diagram.
      

      Since the administration recently had a very large step increase in the rules, they do not want any change. Thus, R(s)=0. The student body does not like the recent changes, so to increase freedom they propose that:

      

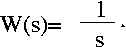
      Use the final value theorem to compute the steady state value of y(t) where R(s)=0 and W(s)=1/s, as specified above.

      1. Enter the value you computed here: y_ss = (5 points)
      2. Use the step command in Matlab to verify that the value you computed is correct (and be sure to submit the plot). (5 points)

   2. In the second model, the administration uses feedback by measuring Y(s) to determine what their response will be, as illustrated in the following block diagram:
      ,

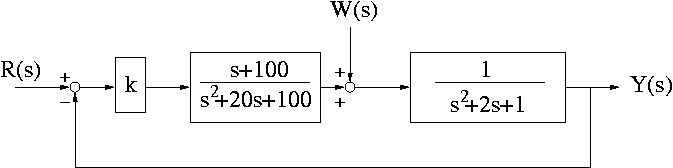      where k=REPLACEq1. Again, use the final value theorem to compute the steady state value of y(t) for the same case where R(s)=0 and W(s)=1/s.

      1. Enter the value you computed here: y_ss = (5 points)
      2. Use the step command in Matlab to verify that the value you computed is correct. (5 points)
      3. Has adding feedback increased or decreased the effect of W(s) on the final value of y(t)? (increased/decreased) (5 points)

   3. The administration is very pleased with your brilliant work using the feedback model. However, the student body has offered you a more attractive compensation package for your services than the administration, so you have started working for them instead. What advice would you give to the students in terms of changing the type or form of the input, W(s), in order to have a greater effect on Y(s)? (5 points)

2. A more complete description of the administration's policy-making procedure is given by the following block diagram where A(s) represents the President and Athletic Director, B(s) represents the French department and the bureau des affaires d'etudiant, C(s) represents the Provost's Office and Burger King and D(s) represents OIT and the Notre Dame Security/Police (notice the relative lack of either student or faculty transfer functions).

   Determine the transfer function Y(s)/R(s) for the following block diagram. (20 points)

   

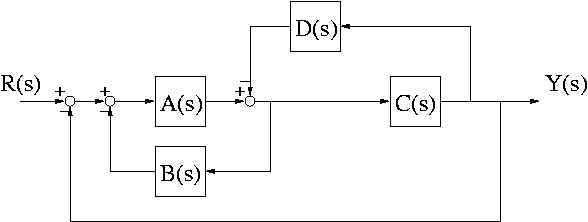
   Enter the transfer function here (in a form like Y/R = (ABC)/(D+ABC)):

   In order to receive any partial credit for an incorrect answer, be sure to submit sketches of any intermediate drawings and computations you have made to derive your answer.

3. Your consulting services are also required by the athletic department due to erratic performance of certain teams.

   Consider the following block diagram.

   

   One coach desires that the rise time of the response of this system to a unit step input be less than 0.9 seconds and that the percentage overshoot be less than 5 percent. Hint: (s+10)(s+11)(s²+2s+2) = s⁴+23s³+154s²+262s+220.

   1. Is it possible to achieve this using proportional control, i.e., D(s) = k? (10 points)

      Enter yes or no:

      Be sure to submit any plots and/or computations to justify your answer.

   2. Design a lead compensator to meet or exceed these performance specifications (to exceed the specifications, you will want a lower rise time and percentage overshoot).
      1. Enter the location of the zero of the lead compensator here: (5 points)
      2. Enter the location of the pole of the lead compensator here: (5 points)

      3. Enter a value of the compensator gain (the K value) that meets or exceeds the performance specifications here: (10 points)
      4. Submit a root locus plot which illustrates that your compensator achieves the desired objectives (10 points).

   3. Assumed you were asked to design a lag compensator so that the steady state error to a step was reduced by a factor of 10. Choose a location for the pole and zero of a lag compensator that would accomplish this. Do not actually compute e_ss for this system -- just say where you would put the compensator pole and zero.
      1. Enter the location of the zero of the lag compensator here: (5 points)
      2. Enter the location of the pole of the lag compensator here: (5 points)

When you are done, hit the "Submit" button. After you hit this button, you will not be able to change any of your answers. All that you are allowed to do is print any computer-generated plots.