Unless otherwise indicated, all the problems are from the course text, Craig, Introduction to Robotics. Unless otherwise indicated, each problem is worth 10 points.

1. Each project group must turn in a summary of the work accomplished to date on Project 2. Attach this to the homework for only one group member -- everyone will get the same credit.
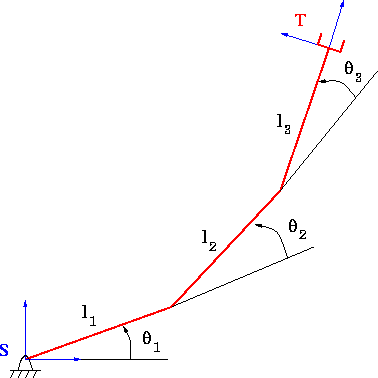
2. For the three link planar robot illustrated in in the Figure,
   1. determine the forward kinematics from the base frame, S, to the tool frame T including the orientation of the tool frame (in class, I only did (x,y));
   2. compute the Jacobian;
   3. determine at least two singular configurations; and,
   4. modify the animation code presented in class to drive the mechanism from the starting configuration given in the code along a desired trajectory that takes it near one of the workspace interior singularities. Verify that large joint velocities occur near the singularity.
   
3. In class, singularities were presented as a generally bad thing since very large joint velocities were required near them. However, they are good in the sense that they maximize mechanical advantage. Show this for the mechanism in the previous problem by finding a large force (and/or torque) near one of the singular configurations that requires very small joint torques to maintain.
4. In Homework 2, you determined the forward kinematics for the mechanism in problem 3.18, Figure 3.38. Assume that we are interested in the (x,y,z) location of the end effector (note that you will have to add a frame at the end effector -- before your forward kinematic computations only went to the frame attached to the last link at the axis of rotation). Assume the reference configuration is as illustrated in the figure in the book.
   1. Compute the Jacobian for this system;
   2. determine at least one singular configuration; and,
   3. if each joint angle is 30^o, and a force, F = (25,25,25) is applied at the origin of the end effector frame, what are the joint torques required to maintain the force?
5. In Homework 2, you determined the forward kinematics for the mechanism in problem 3.20, Figure 3.40. Assume that we are interested in the (x,y,z) location of the end effector. Assume the reference configuration is as illustrated in the figure in the book.
   1. compute the Jacobian for this system;
   2. determine at least one singular configuration; and
   3. if each joint angle is 30^o, and a force, F = (25,25,25) is applied at the origin of the end effector frame, what are the joint torques required to maintain the force?
6. In Homework 3, you determined the forward kinematics for the mechanism in problem 3.21, Figure 3.41. Assume that we are interested in the (x,y,z) location of the end effector. Assume the reference configuration is as illustrated in the figure in the book. What are the singular configurations for this mechanism?
7. (Wait until afer Wednesday's class to attempt this one).
   Consider the four dimensional SCARA type robot considered in class last week. Assume that each of the three rotational joints is at 30^o, and the prismatic joint is at the reference configuration, i.e., theta_4 = 0.
   1. What is the direction of the maximum mechanical advantage?
   2. What is the direction of the maximum velocity amplitude?