This project will use a calibration approach to using vision for robot manipulator control. This is in contrast with "Camera Space Manipulation" which is the subject of Dr. Skaar's research. Calibration methods suffer from several shortcomings; on the other hand, it is perhaps the predominant methods of vision based robotic control in industry. (See the Adept vision robots.)

Your contribution to the project will be two C programs and subsequent testing of the calibration approach. The first program is a thresholding program. It must be satisfy the following requirements:

1. The executable thresholding program must be called thresh and be located in /home2/freak on me469.ame.nd.edu Note: you must compile it using gcc on me469.
2. The program must take two command line argument (which are specified internally by the puma GUI control program):
   1. the first argument (argv[1]) is the filename of the pgm image file to be thresholded;
   2. the second argument (argv[2]) is the threshold level (use atoi(argv[2]) to convert the command line argument to its integer value);
   3. normally, thresholding converts all pixels at and above the threshold value to 255 and all pixels below the threshold value to 0; however, in this implementation, all pixels below the threshold value will be assigned the value of 100 (so they will appear gray instead of black).
3. The output of the program must be written to a file named out.pgm.th.

thresh out.pgm 150 
	      

thresh what.pgm 85 
	      

A camera located above the robot can acquire images of the robot and its workspace via the GUI. There is a black triangle located on the end effector, and the goal, as described subsequently, is to locate the pixel values of the tip of the triangle. After thresholding, the image will have white regions (255) and gray regions (100). The triangle will be gray, as well as other dark areas in the image. The user identifies the triangle by clicking on it. The GUI can determine the pixel values that the user clicked, and then passes these values to your second program, which implements a modified version of the connect component labeling algorithm.

The purpose of your second program is to identify the pixel values (row and column values) corresponding to location of the tip of the triangle in the thresholded image. This is accomplished via the following steps:

1. The GUI calls your second program, and tells it the values of the clicked point (which are somewhere inside the triangle).
2. The program sets the pixel value of the corresponding location to 0 (black).
3. Proceeding from left to right and top to bottom, the program looks for pixel values of 100 (corresponding to pixels below the threshold value) with a 4-neighbor with a value of 0. If it has such a neighbor, its value it changed to 0 as well.
4. Proceeding from right to left and bottom to top, the program looks for pixel values of 100 (corresponding to pixels below the threshold value) with a 4-neighbor with a value of 0. If it has such a neighbor, its value it changed to 0 as well.
5. The previous two steps are repeated until no pixel values are changed. At this point, all the pixels with a value of 100 that were connected to the clicked point will have a value of 0, and the triangle (assuming the user clicked on it) will be black, the other areas under the threshold value will be gray (100) and the pixels above the threshold value will be white.
6. Next, the program computes the area of the triangle (which is now the set of black pixels) and its centroid.
7. Once the centroid is identified, the tip should be the black pixel that is located the furthest distance away from the centroid.

To interface with the GUI, your program must satisfy the following requirements:

1. The executable must be called triangle and be located in /home2/freak on me469.ame.nd.edu. As before, you must compile it using gcc on me469.
2. The program must accept three command line arguments:
   1. the first argument will be the filename of the thresholded image (the image is exactly the same as out.pgm.th, the output of your thresholding program, but the GUI actually changes the name);
   2. the second argument is the row value of the clicked point (identifying a point in the triangle);
   3. the third argument is the column value of the clicked point.
3. The program must print out to a file called out.pgm.th2 the image in which all the gray pixels in the input file that are connected to the clicked point are changed to black.
4. The program must print, using

   printf("%d %d %d %d\n",ctip,rtip,ccent,rcent)

   in exactly the following order, the values of
   1. the column value of the tip of the triangle;
   2. the row value of the tip of the triangle;
   3. the column value of the centroid of the triangle;
   4. the row value of the centroid of the triangle;
   so that they can be acquired by the GUI.

Here are three sets of sample images. The first image is the captured image, the second is after thresholding and the third is after the triangle has been identified.

1. First image:
   1. Captured image.
   2. Thresholded image.
   3. Triagle image.
      Clicked coordinates were: col = 280, row = 259.
      Computed tip coordinates were: col = 198, row = 269.
2. Second image:
   1. Captured image.
   2. Thresholded image.
   3. Triagle image.
      Clicked coordinates were: col = 230, row = 112.
      Computed tip coordinates were: col = 161, row = 122.
3. Third image:
   1. Captured image.
   2. Thresholded image.
   3. Triagle image.
      Clicked coordinates were: col = 349, row = 202.
      Computed tip coordinates were: col = 291, row = 210.

After your programs run, they are used to control the robot in the following manner.

To calibrate the vision based controller for the robot, you will move the robot to a set number of configurations and instruct the controller to save the image location of the robot as well as its actual position in the plane. After the samples are saved, the robot can be instructed to move to any image location. The controller computes the actual location by interpolating between or extrapolating from x and y coordinates saved in the calibration step.

There are a variety of ways of using calibrated points to control the robot, but here we will use a particularly simple approach. What the controller does is find the two closest saved sample points, and does a simple linear interpolation separately for the x and y components of each.

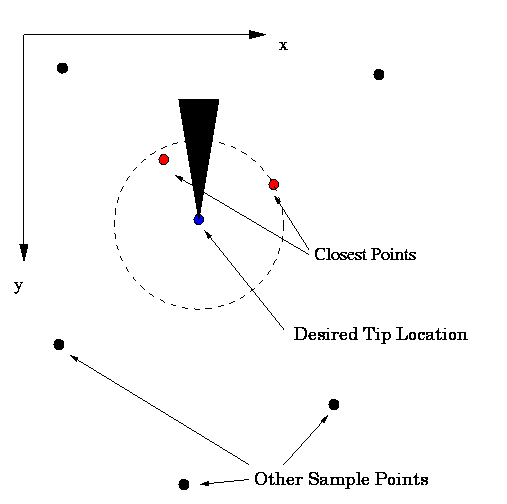
Each of the two closest points will have image and world coordinates, respectively: (x_1,image,y_1,image), (x_2,image,y_2,image), (x_1,world,y_1,world), (x_2,world,y_2,world). Let the desired tip image location be specified by (x_des,y_des). Then simple, coordinate decoupled interpolation gives the world tip locations by

While seemingly straightforward, this method is fundamentally flawed in a couple of ways. Hopefully your experimentation will discover some of these. The purpose of this lab is to explore the efficacy of the vision based calibration control strategy described above.

Details:

1. Log on to me469.ame.nd.edu using the same username and password as for the second project.
2. Start the GUI by typing

          puma
   	

3. Initialize the robot by following the instructions under the initialize command under the file menu.
4. After initializing, the vision window is started under the vision file menu.
   1. The "Capture" button captures a new image;
   2. The "Threshold" button thresholds the image;
   3. To highlight the triangle on the "forklift" click on the triangular region. This will identify the triangle and compute the coordinates of the tip of the triangle as well as its centroid. Note: be patient. The connected components algorithm which identifies the triangle can take a long time. If the triangle is not highlighted as black after about 15 seconds you either didn't exactly click on the triangle or there is some other problem. Just capture another image and try again.
   4. The "Save Sample" button saves the tip and centroid coordinates as well as the configuration of the robot. In order to be used in the calibration calculations, the samples must differ from each other by at least 10 pixels in both the x and y directions for the tip of the triangle. If you do not hit the "Save Sample" button, no information is saved regarding the current image.
5. After saving some samples the "Calibrated Motion" button will cause the robot to move to any location specified by clicking on the image plane. In order for the GUI to control the location of the arm, the robot must be under computer control, so you have to hit the "comp" button on the teach pendant, if you have been using the "world" mode to move it between calibration points.
6. After setting everything up and getting it to seemingly work properly, see how well such a calibration based approach works by saving 2,4,8 and possibly more samples, and in each case record the following data:
   1. The location and number of calibration points (these should appear in the puma control window);
   2. The location of several calibrated motion points and an indication of the amount of error, if measurable, associated with the motion;
   3. A qualitative characterization of the error, e.g.,
      1. Is the error biased in a particular direction (left, right, up or down)?
      2. Is the error greater in a particular region of space or a particular region of the image, e.g., in the periphery or the center of the image?
      3. Is the error greater if the controller has to extrapolate from the calibration points rather than interpolate between them?
      4. Does is matter where the calibration point are located? For example, for the case of 4 calibration points does the system work better or worse if they are clustered together or spread apart? Does it matter if they are arranged in a line or a polygon? Try, for example, to calibrate four points in a square near the center of the grid and then calibrate in a square using the four extreme corners of the grid. Does one way work better than the other, does each work just as well, or does each have relative advantages and disadvantages?
      5. To the extent there is error present, can you identify a likely source?
      6. etc.
   4. After testing the system with 8 calibration points, if you think that better performance will be gained by saving even more points, try it with more calibration points.
   5. Finally, calibrate the system with enough points so that it works with reasonable accuracy. Then move the camera slightly (about 1/2 inch) in any direction. How much did this impact the accuracy of the system?
7. Write a concise, coherent and otherwise brilliant project report.

Return to the AME 469 Homepage.