University of Notre Dame
Aerospace and Mechanical Engineering

ME 654: Geometric Nonlinear Control
Homework 4

B. Goodwine Fall, 2003

Issued: August 28, 2003 Due: September 25, 2003

1.

Consider the motion of a particle of mass m attached to a spring with a nonlinear stiffness k (x + x³), k > 0, where x is the displacement. The differential equation governing the system is

$$m \ddot x + k (x + x^3) = 0.$$

(a)

Using the total energy as a Lyapunov function, what can you conclude about the stability of the system?

(b)

If damping is added to the system in the form

$$\ddot x + \alpha \dot x + k (x + x^3) = 0 \qquad \alpha > 0,$$

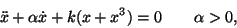
what can you conclude about the stability of the system?

2.

Using the Lyapunov function

$$V = \frac{1}{2} \left( x^2 + \sigma y^2 + \sigma z^2 \right)$$

obtain conditions on $\sigma$, $\rho$ and $\beta$ sufficient for global asymptotic stability of the origin (x, y, z) = (0,0,0) in the Lorenz equations

$$\begin{eqnarray*}\dot x &=& \sigma (y - x) \\ \dot y &=& \rho x - y - x z \\ \dot z = - \beta z + x y, \end{eqnarray*}$$

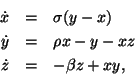
where $\sigma, \beta > 0$.

3.

Investigate the stability of the origin of

$$\begin{eqnarray*}\dot x_1 &=& \left( x_1 - x_2 \right) \left( x_1^2 + x_2^2 - 1 ... ..._2 &=& \left( x_1 + x_2 \right) \left( x_1^2 + x_2^2 - 1 \right) \end{eqnarray*}$$

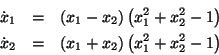
using a Lyapunov function of the form

$$V(x) = \alpha x_1^2 + \beta x_2^2.$$

4.

Consider the linear first order system

$$\dot x = - \frac{x}{1+t}.$$ (1)

(a)

Show that

$$\begin{eqnarray*}x(t) &=& x(t_0) \exp \left( \int_{t_0}^t \frac{-1}{1+\tau} d \tau \right)\\ &=& x(t_0) \frac{1+t_0}{1+t} \end{eqnarray*}$$

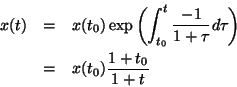
is the solution of the differential equation.

(b)

Is the origin a stable fixed point?

(c)

Is the origin an asymptotically stable fixed point?

(d)

Is the origin a uniformly asymptotically stable fixed point?

In each case, justify your answer.

5.

Investigate the stability of the origin of

$$\begin{eqnarray*}\dot x &=& y - \sin^3 x\\ \dot y &=& - 4 x - \sin^3 y \end{eqnarray*}$$

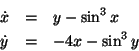
using a Lyapunov function of the form

$$V = x^2 + \alpha y^2.$$

6.

Show that the zero solution of

$$\ddot x + h(x, \dot x) \dot x + x = 0$$

is stable if $h(x, \dot x) \geq 0$ in a neighborhood of the origin.

7.

Investigate the stability of the origin of

$$\begin{eqnarray*}\dot x_1 &=& - x_1 - x_2\\ \dot x_2 &=& x_1 - x_2^3. \end{eqnarray*}$$

8.

Using the simple example of

$$\dot x = - 3 x,$$

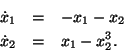
work through the proof of case 3 in the table of Lyapunov theorems in Sastry's text.

Oysters are supposed to be the first course. Or terrapin. Then the soup, then the fish, then the mushrooms or asparagus, then the roast, then the frozen punch, then the game, then the salad, then the creamed dessert, then the frozen dessert, then the cheese, then the fruit, and then hungry guests can get into the candy and nuts.

--- Judith Martin (Miss Manners), August 21, 1996.

Last updated: September 17, 2003.
B. Goodwine (jgoodwin@nd.edu)