near
-
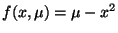
-
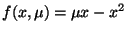
-
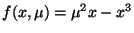
-
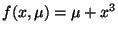
-
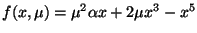 for various
for various 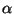 .
.
- Use the conditions on
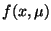 derived in class or on the
handout to try to determine the type of bifurcation.
derived in class or on the
handout to try to determine the type of bifurcation.
- Construct the bifurcation diagram.
| B. Goodwine
Fall, 2003 |
Issued: August 28, 2003 Due: October 9, 2003 |
Amicus Plato amicus Aristoteles magis amica veritas. [Plato is my friend, Aristotle is my friend, but my best friend is truth.]
--- Isaac Newton, undergraduate notebook, 1664.