University of Notre Dame
Aerospace and Mechanical Engineering
AME 30314: Differential Equations, Vibrations and Controls I
Fall 2015
Homework 2, due September 9, 2015
Problem 1
Determine the solution to
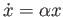 where
where  .
On the same graph, sketch the solution for
.
On the same graph, sketch the solution for
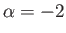 ,
,
 ,
and
,
and
 .
.
Problem 2
In dead organic matter, the 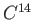 isotope decays at a rate
proportional to the amount of it that is present. Furthermore, it
takes approximately 5600 years for half of the original amount present
to decay.
isotope decays at a rate
proportional to the amount of it that is present. Furthermore, it
takes approximately 5600 years for half of the original amount present
to decay.
- If
 denotes the amount present when the organism is alive,
determine a differential equation that describes the amount of
the
denotes the amount present when the organism is alive,
determine a differential equation that describes the amount of
the 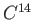 isotope present if
isotope present if 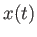 represents the amount present after
time
represents the amount present after
time 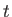 elapses after the organism dies.
elapses after the organism dies.
- In contrast to
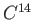 , the
, the 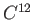 isotope does not decay and
the ratio of
isotope does not decay and
the ratio of 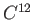 to
to 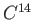 is constant while an organism is
alive. Hence, one should be able to compare the ratio of the two
isotopes in a dead specimen to that of a live specimen. Determine
how many years have elapsed if the ratio of the amount of
is constant while an organism is
alive. Hence, one should be able to compare the ratio of the two
isotopes in a dead specimen to that of a live specimen. Determine
how many years have elapsed if the ratio of the amount of 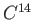 to
to 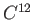 is
is  of the original value.
of the original value.
Do not look up the formula for half-life and exponential decay
problems. The point is to derive the equation in order to relate it
to the problem, and then to solve it.
Problem 3
Consider the first-order, linear, variable-coefficient, homogeneous
ordinary differential equation
Does assuming a solution of the form
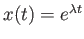 where
where
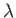 is a constant work? Why or why not?
is a constant work? Why or why not?
Problem 4
Consider the first-order, nonlinear, ordinary differential equation
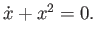 Does assuming a solution of the form
Does assuming a solution of the form
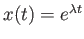 work? Why or why not?
work? Why or why not?
Problem 5
As part of a fabrication process, you encounter the following
scenario. A vat contains 50 liters of water. In error someone pours
100 grams of a chemical into the vat instead of the correct amount,
which is 50 grams. To correct this condition, a stopper is removed
from the bottom of the vat allowing 1 liter of the mixture to flow
out each minute. At the same time, 1 liter of fresh water per minute
is pumped into the vat and the mixture is kept uniform by constant
stirring.
- Show that if
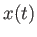 represents the number of grams of chemical in the
solution at time
represents the number of grams of chemical in the
solution at time 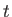 , the equation governing
, the equation governing 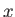 is
is
where
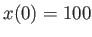 .
How long will it take for the mixture to contain the desired
amount of chemical?
.
How long will it take for the mixture to contain the desired
amount of chemical?
- Determine the equation governing
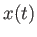 if the amount of water
in the vat is
if the amount of water
in the vat is  liters, the rate at which the mixture flows out is
liters, the rate at which the mixture flows out is 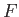 liters/minute (and the same amount of fresh water is added), and the
amount of the chemical initially added is
liters/minute (and the same amount of fresh water is added), and the
amount of the chemical initially added is  grams.
grams.
Problem 6
The rate by which people are infected by the zombie plague is
proportional to the number of people already infected. Let 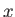 denote the number of people infected.1
denote the number of people infected.1
- What is the differential equation describing the number of
people infected? Denote the proportionality constant by
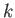 . What are
the units for
. What are
the units for 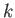 in the differential equation? What is the general
solution to this equation? What are the units for
in the differential equation? What is the general
solution to this equation? What are the units for 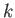 in the solution?
in the solution?
- If at time
 there are 100,000 people infected and at time
there are 100,000 people infected and at time
 (the next day) there are 225,000 people infected, what is the
numerical value of
(the next day) there are 225,000 people infected, what is the
numerical value of 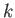 ?
?
- For the value of
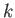 determined in the previous part, if at time
determined in the previous part, if at time
 , one person is infected, how long will it take for the zombie
plague to infect every person on earth?
, one person is infected, how long will it take for the zombie
plague to infect every person on earth?
Problem 7
Assume that the rate of loss of a volume of a substance, such as dry
ice or a moth ball, due to evaporation is proportional to its surface
area.
- If the substance is in the shape of a sphere, determine the
differential equation describing the radius of the ball and solve it
to find the radius as a function of time.
- If the substance is in the shape of a cube, determine the
differential equation describing the length of an edge of the cube and
solve it to find the length of the edge as a function of time.
- Use the answers from the previous two parts to determine which
shape would be better for a given quantity of material if it is
desired for it to take as long as possible to evaporate.
Problem 8
Match the following differential equations with the solutions plotted in the figure without actually solving the equation. Explain your reasoning for each one.
-
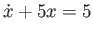 .
.
-
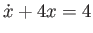 .
.
-
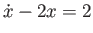 .
.
-
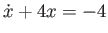 .
.
-
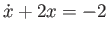 .
.
Figure 1:
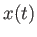 solutions
solutions
|
|
2015-09-04
![]() isotope decays at a rate
proportional to the amount of it that is present. Furthermore, it
takes approximately 5600 years for half of the original amount present
to decay.
isotope decays at a rate
proportional to the amount of it that is present. Furthermore, it
takes approximately 5600 years for half of the original amount present
to decay.
![]() Does assuming a solution of the form
Does assuming a solution of the form
![]() work? Why or why not?
work? Why or why not?
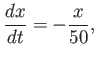
![]() denote the number of people infected.1
denote the number of people infected.1