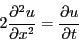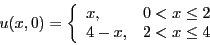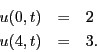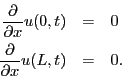Bill Goodwine's Courses

1. Consider the one dimensional heat conduction equation
   • 
   with
   • 
   subjected to
   • 
   1. Determine the solution u(x,t).
   2. Write a computer program to determine an approximate numerical solution for u(x,t).
   3. Compare the two solutions by plotting the solution for several times.
2. If the bar has ends that are insulated instead of held at a constant temperature, then the boundary conditions are that the derivative of the temperature at the ends must be zero.
   1. Use the method of separation of variables to solve the one dimensional heat equation given above with the same initial temperature profile, but, instead of having the ends held at a fixed temperature insulated ends expressed by the following boundary conditions
      • 
   2. Write a computer program to find an approximate numerical solution for this system.
   3. Compare the two solutions by plotting the solution for several times.

msudyk wrote:in the program done in class you used dx = 0.2, and the do loop goes to 100, should the dx = 0.02 instead so that it spans 0-2 not 0-20?