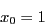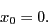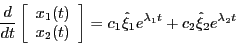Bill Goodwine's Courses

Consider

• 

1. Determine a linear differential equation that is a good approximation of this one near the points
   • 
   and
   • 
2. Near each of those points, find the analytical solution to this linear approximation.
3. Near the point
   • 
   make a plot on the phase plane of the linear solution and the nonlinear solution (determined numerically using whatever method you want, including matlab) for various initial conditions. Include a plot of the solutions where the initial conditions are such that the linear solution is a good approximation to the nonlinear solution; one where it is a terrible approximation and one that is intermediate.
4. Near the point
   • 
   write the analytical solution in the form of
   • 
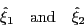   where are vectors and x1 and x2 are x(t) and the derivative of x(t) respectively.
   
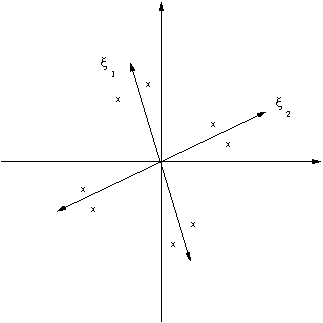
   Plot these vectors. Plot (-1) times these vectors. Compare the linear and nonlinear solutions for 8 different initial conditions, one close to and on each side of the vectors plotted, as indicated by the "x"s illustrated in the following figure.
   
   • 
   Note: all of these solutions will blow up. Restrict the plot to be between plus and minus 2 for each axis. You may have to fiddle with the total time of the simulation to make sure it runs long enough to leave the range of the plot but not too long so that the simulation dies.

When we are finding the linear approximation to the nonlinear equation, how do we know what value of xdot(0) to use? In the examples you did in the text, you chose xdot(0)=10.2 for one and xdot(0)=0.2 for another and I'm not sure how you picked those values.

aoconno5 wrote:When we are finding the linear approximation to the nonlinear equation, how do we know what value of xdot(0) to use? In the examples you did in the text, you chose xdot(0)=10.2 for one and xdot(0)=0.2 for another and I'm not sure how you picked those values.

If the equation is linear in xdot, then it should not matter what you use; however, if xdot is large, then x will be changing a lot so it may not be likely to hang around x_0. Hence, it's usually a good ideal to make xdot small.

There shouldn't be a d/dt in front of the [x1, x2] vector. That is the solution, not the original differential equation.

Not all of the solutions blow up, but most of them do.