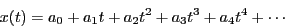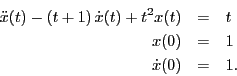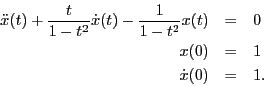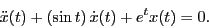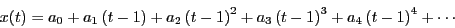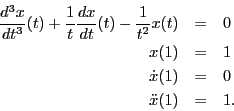Homework 6, due October 15, 2008.

[goodwine]

1. Assume a solution of the form
   • 
   to find a series solution to
   • 
   Plot the solution for the first four and then five terms. Based upon the plot, what seems to be the range of time for which the series solution with the first 4 terms is valid?
   Hint: you could use a power series for the homogeneous solution and then undetermined coefficients for the particular solution, but since the inhomogeneous term is t you might was well just include it when you determine the coefficients in the power series.
2. Write a computer program that uses Euler's method to compute an approximate numerical solution for the equation in the previous problem. On the same plot, plot the numerical solution and the power series solutions.
3. Assume a solution of the form
   • 
   to find a series solution to
   • 
   Plot the solution for the first four and then five terms. Based upon the plot, what seems to be the range of time for which the series solution with the first 4 terms is valid?
4. Write a computer program that uses Euler's method to compute an approximate numerical solution for the equation in the previous problem. On the same plot, plot the numerical solution and the power series solutions.
5. Assume a solution of the form
   • 
   to find the first five terms in the series for the general solution to
   • 
   Hint: expand the sine and exponential functions in their Taylor series.
6. Assume a solution of the form
   • 
   to find a series solution to
   • 
   Plot the solution for the first four and then five terms. Based upon the plot, what seems to be the range of time for which the series solution with the first 4 terms is valid?
   Hint: you want to equate powers of (t-1), not t.
7. Write a computer program that uses Euler's method to compute an approximate numerical solution for the equation in the previous problem. On the same plot, plot the numerical solution and the power series solutions.
8. Extra credit: (5 points each) for each of the problems determine a general form for the series (with a summation sign and an index on the coefficients).
9. Extra credit: (5 points each) if you did the previous extra credit for each one, use your answers there to compute the range of times for which the power series will converge.
10. Extra credit: (5 points each) for the problems where initial conditions were specified, plot the series solutions for 25, 50, 75 and 100 terms and compare with the approximate numerical solutions.

Notes:

1. I have not done the extra credit problems myself (yet). Sometimes they can be pretty hard to work out; other times, not so much. At this point I don't know which case it is for any of these problems.
2. The usual rules for programs apply: you must use Fortran, C or C++ for the program to determine approximate numerical solutions using Euler's method. You may use Matlab for all the plots.
3. If the problem asks you to plot four and then five terms in the series, if one of the coefficients happens to be zero so that you are plotting exactly the same thing, then you must keep including more terms until you plot the next higher non-zero term in the series. The point is to add a term to see how it changes, which should indicate the range in which the truncated series is a good approximation. This shouldn't be confused with the range of convergence of the whole (infinite) series.

[bboston]

In problem 3 and 4, how do you deal with the discontinuity at t=1? In the fortran numerical solution, the plot blows up because its a divide by zero at t=1, so should we plot twice, once for 0<t<1 and t>1?

Thanks

[goodwine]

In problem 3 and 4, how do you deal with the discontinuity at t=1? In the fortran numerical solution, the plot blows up because its a divide by zero at t=1, so should we plot twice, once for 0<t<1 and t>1?

You could do that, or just do it for less than 1. Since there is a singularity at t=1, the neither solution (numerical nor series) is probably valid through that point.

[goodwine]

On problem 5 in the hw I believe that we need initial conditions to solve for the first five terms of the series and none are given. Should we assume that x(0) = 1 and xdot(0) = 1 or are these not necessary to solve the problem.

You are supposed to find the general solution, so leave everything in terms of a0 and a1.

[sjensen1]

In problem 8, how do we deal with powers of t? Are the coefficients going to be in terms of t?

[goodwine]

In problem 8, how do we deal with powers of t? Are the coefficients going to be in terms of t?

Do you mean problem 6? If so, expand the terms 1/t and 1/t^2 in a Taylor series about t=1, then you can equate powers of (t-1).

[drudy]

in problem 6, after you expand 1/t and 1/t^2 to their Taylor series and combine with dx/dt and x, won't you have powers of (t-1)^(2n) but d^3x/dt^3 will have a power of (t-1)^n. is there a way to get all the terms back to (t-1)^n?

[goodwine]

in problem 6, after you expand 1/t and 1/t^2 to their Taylor series and combine with dx/dt and x, won't you have powers of (t-1)^(2n) but d^3x/dt^3 will have a power of (t-1)^n. is there a way to get all the terms back to (t-1)^n?

At that point I think you just want to write out the first few terms of each series and equate the coefficients. Doing it in a general form is maybe very difficult.