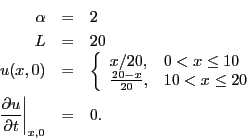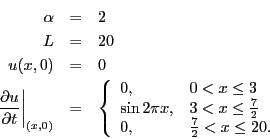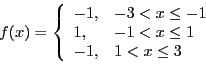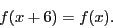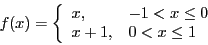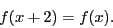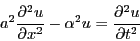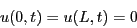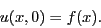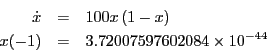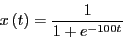Bill Goodwine's Courses

Reading: Chapter 12 in the course text.

Exercises:

1. Determine the solution to the wave equation where
   • 
   Plot the solution for t=0 and several other times to clearly demonstrate the nature of the solution.
   
   Extra credit: make a movie of the solution.
2. Determine the solution to the wave equation where
   • 
   Plot the solution for t=0 and several other times to clearly demonstrate the nature of the solution.
   
   Extra credit: make a movie of the solution.
3. Compute the Fourier series for
   • 
   where
   • 
   Plot f(x) and the first several terms of the series on the same graph.
4. Compute the Fourier series for
   • 
   where
   • 
   Plot f(x) and the first several terms of the series on the same graph.
5. Determine the solution to
   • 
   where
   • 
   and
   • 
   You may assume the initial velocity profile is zero.
6. Consider the differential equation
   • 
   1. Show that
      • 
      is the solution to the differential equation.
   2. Write a computer program to determine an approximate solution using the 4th order R-K method to this first order differential equation.
   3. Submit a plot of the approximate solution and the exact solution for this equation for the time interval from t=-1 to t=1. Use trial and error to determine an appropriate step size by comparing your approximate numerical solution to the exact solution for different step sizes and ensure that the magnitude of the maximum error is less than 0.001. Hint the step size has to be pretty small! Be sure to submit your code as well.
   4. Use the Matlab ode45() function to solve the equation. Submit your code and a plot of the solution and the exact solution. Does Matlab give the correct answer?
   5. (5 points extra credit) Figure out how to tweak the tolerances in ode45(). Is it possible to get an accurate solution?
   6. Write a matlab script to implement Euler's method to determine an approximate numerical solution to the above "innocent" equation. An example script using Euler's method to solve the equation
      • 
      would look like the following:

      Code: Select all

      >> x(1) = -6;
      >> dt = 0.01;
      >> t = 0:dt:10;
      >> for i=2:length(t)
      x(i)=x(i-1)+sin(t(i-1))*dt;
      end
      >> plot(t,x)
      

      Using this script and Euler's method. Approximately determine how long it would take for the script to run to return an approximate solution that is as accurate as your code from above.

should we plot the equation for number 2 about some other point then t=0 because the position is always 0 at t=0? or should we plot the velocity?

In problem 5, are both a's the same or is the first an "a" while the second is an alpha on purpose?

sagarwal wrote:should we plot the equation for number 2 about some other point then t=0 because the position is always 0 at t=0? or should we plot the velocity?

It says several other times too. So, a plot showing it at zero, and then some other times, which should show that the motion starts at the area where the velocity is not zero, and then some plots to show the nature of how it moves. You probably want to loop through time anyway in the plotting program, so the t=0 plot shouldn't be any more work.

satkinso wrote:In problem 5, are both a's the same or is the first an "a" while the second is an alpha on purpose?

Yes, they are different.

Professor, I'm having trouble understanding how to plot the solutions for u(x,t). Do I use my loop to change x, take n=1 and make multiple plots by rerunning with different t values?

There are many ways to do it. I would fix t, then plot it versus x. You will need to include quite a few terms in the series to ensure that what you plot represents the actual solution.

Professor Goodwine,

I'm having trouble following an example in the book. With Equations 12.19 & 12.20 they have sin(n*pi*x/L) and cos(n*pi*x/L) respectively, but in Example 12.2.5 on page 389 when solving for both a_n and b_n a 2 is in the numerator. I'm sure I'm just missing a simple step but is there any chance you could explain it? Thanks!


Bristol

bristolschmitz wrote:I'm having trouble following an example in the book. With Equations 12.19 & 12.20 they have sin(n*pi*x/L) and cos(n*pi*x/L) respectively, but in Example 12.2.5 on page 389 when solving for both a_n and b_n a 2 is in the numerator. I'm sure I'm just missing a simple step but is there any chance you could explain it? Thanks!

I'm not sure why the 2 is in the denominator, but the second line in each set of equations seems to be correct. L=1 is what should be used.

Why is it that the integrations in example 12.2.5 go from 0 to 2, but equations 12.19 and 12.20 use -L to L? Should the integrations in the example go from -1 to 1, or doesn't it matter as long as the integration goes over a whole period?

...Oh nevermind...it's in the book! Thanks!

How can we submit our movies to you? Mine have the extension .wmv which is not allowed to be attached to our submissions...

Professor Goodwine,

For problems 3 and 4, should we be putting in combinations of the first several terms of the series (so you see the solution getting closer) or just the first several terms separately. It says the first several terms, but I wasn't sure if you meant the combination of the first several terms. Thanks,

Ian