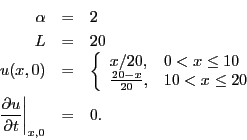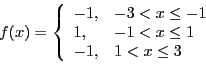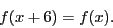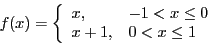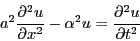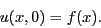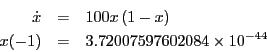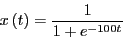Bill Goodwine's Courses

Reading: Chapter 12 in the course text.

Exercises:

1. Determine the solution to the wave equation where
   • 
   Plot the solution for t=0 and several other times to clearly demonstrate the nature of the solution.
   
   Extra credit: make a movie of the solution.
2. Determine the solution to the wave equation where
   • 
   Plot the solution for t=0 and several other times to clearly demonstrate the nature of the solution.
   
   Extra credit: make a movie of the solution.
3. Compute the Fourier series for
   • 
   where
   • 
   Plot f(x) and the first several terms of the series on the same graph.
4. Compute the Fourier series for
   • 
   where
   • 
   Plot f(x) and the first several terms of the series on the same graph.
5. Determine the solution to
   • 
   where
   • 
   and
   • 
   You may assume the initial velocity profile is zero.
6. Solve the heat equation with homogeneous boundary conditions with alpha=1, L=4 and a uniform initial temperature of u=1. Plot the solution for various times to illustrate the nature of the solution.
7. Solve the heat equation with homogeneous boundary conditions with alpha=2, L=2 and an initial temperature distribution that is triangular, zero at both ends and with a peak of u=2 in the center. Plot the solution for various times to illustrate the nature of the solution.
8. Consider the differential equation
   • 
   1. Show that
      • 
      is the solution to the differential equation.
   2. Write a computer program to determine an approximate solution using the 4th order R-K method to this first order differential equation. Write your program so that it saves 1000 data points to a file, i.e., don't save every single step. Write the program so that if you change either the time step size or the total time for the simulation, it computes how to save 1000 points. In other words, don't hard code into your program some logic that only works for a specific step size and specific final time.
   3. Submit a plot of the approximate solution and the exact solution for this equation for the time interval from t=-1 to t=1. Use trial and error to determine an appropriate step size by comparing your approximate numerical solution to the exact solution for different step sizes and ensure that the magnitude of the maximum error is less than 0.001. Hint the step size has to be pretty small! Be sure to submit your code as well.
   4. Use the Matlab ode45() function to solve the equation. Submit your code and a plot of the solution and the exact solution. Does Matlab give the correct answer?
   5. (5 points extra credit) Figure out how to tweak the tolerances in ode45(). Is it possible to get an accurate solution?
   6. Write a matlab script to implement Euler's method to determine an approximate numerical solution to the above equation. An example script using Euler's method to solve the equation
      • 
      would look like the following:

      Code: Select all

      >> x(1) = -6;
      >> dt = 0.01;
      >> t = 0:dt:10;
      >> for i=2:length(t)
      x(i)=x(i-1)+sin(t(i-1))*dt;
      end
      >> plot(t,x)
      

      If you did this method for the equation in this problem, approximately how long it would take for the script to run to return an approximate solution that is as accurate as your code from above?

If we are making a video for the homework, do we need to post it somewhere for you to actually see that it works or do we just need to print out the code from it?
basically how would you like us to prove the extra credit?

thanks.

charri11 wrote:If we are making a video for the homework, do we need to post it somewhere for you to actually see that it works or do we just need to print out the code from it?
basically how would you like us to prove the extra credit?

If it's smaller than 1MB, email it to me. If it's larger, copy it to your www directory (or facebook or something else like that, if you want) and send a link to it to me.

When you say plot "the first few terms of the series" in problems 3 and 4, do you mean each of the terms individually, like f1(x),f2(x),f3(x) (as done in Figure 12.3 in the text), or collectively (as done in Example 12.2.5 and Figures 12.10,12.11, and 12.12)?

Josh wrote:When you say plot "the first few terms of the series" in problems 3 and 4, do you mean each of the terms individually, like f1(x),f2(x),f3(x) (as done in Figure 12.3 in the text), or collectively (as done in Example 12.2.5 and Figures 12.10,12.11, and 12.12)?

Collectively, to approximate the solution.

For Problem 5:

Using separation of variables, I got an equation where one side depends on x and one side depends on t, meaning each side is a constant. However, I don't know if the constant would be positive or negative. I looked at the wave equation, and that constant was chosen to be negative. Without any intuition about the physical nature of the problem (if the string is above the centerline (X(x)>0) then the curvature should be negative(X''(x)<0), making the constant on the RHS<0), I don't know how to mathematically infer the sign of the constant for the wave equation, let alone the equation for problem 5. It seems that whether it is positive or negative will affect the form of the solution (exponentials or sins and coss, even though they really are the same thing with the imaginary exponents)...

Also, just making sure it is not a typo, alpha and a are separate constants, right?
Thank you

mkiener wrote:For Problem 5:

Using separation of variables, I got an equation where one side depends on x and one side depends on t, meaning each side is a constant. However, I don't know if the constant would be positive or negative. I looked at the wave equation, and that constant was chosen to be negative. Without any intuition about the physical nature of the problem (if the string is above the centerline (X(x)>0) then the curvature should be negative(X''(x)<0), making the constant on the RHS<0), I don't know how to mathematically infer the sign of the constant for the wave equation, let alone the equation for problem 5. It seems that whether it is positive or negative will affect the form of the solution (exponentials or sins and coss, even though they really are the same thing with the imaginary exponents)...

Also, just making sure it is not a typo, alpha and a are separate constants, right?
Thank you

Yes, a and alpha are different.

In general, once things are separated you only know that the resulting sides of the equation are constant, but not whether it is positive or negative. However, it will be the case that it can only be positive or negative and still satisfy the boundary conditions. For example, in the wave equation I did -lambda^2 and everything just worked out ok. If I had just done lambda, then the equation would have been X'' - lambda X = 0, which will have two exponential solutions if lambda is positive and sine and cosine solutions if lambda is negative. It is only the sine and cosine case that can satisfy the boundary conditions.

So, in summary, the boundary conditions force the constant to be either positive or negative.