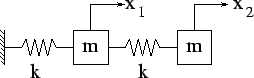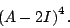Page 1 of 1
Homework 4, due February 16, 2005.
Posted: Fri Feb 11, 2005 5:41 pm
by goodwine
- Consider the system illustrated in the following figure. Assume k=m=1.
- Derive the equations of motion for the system.
- Assuming two solutions of the form
determine two solutions for the frequency and the amplitude ratio of the two responses.
- What is the response of the system if
- Write the equations of motion in the form
- Compute the eigenvalues and eigenvectors of A (using a computer is allowed).
- Determine the general solution of the system in terms of real-valued functions.
- Verify your answer from part c using your solution from this problem.
- Consider
where
- Compute a set of 4 vectors that span the null space of
- For each of the four (generalized) eigenvectors you computed in part a, determine the corresponding homogeneous solution of the form
- Compute a different set of 4 vectors (at least 3 of the 4 must be different) that span the null space of
- Determine the homogeneous solution corresponding to each (generalized) eigenvector from part c.
- Determine the general solution for the system, including the -2 eigenvalue, using your 4 homogeneous solutions from part b.
- Determine the general solution for the system, including the -2 eigenvalue, using your 4 homogeneous solutions from part d.
- The two general solutions shold be different. If
are the solutions to the initial value problem the same? If they are, must they be? Are the two general solutions actually equivalent?
- Find the general solution to
where
by computing homogeneous solutions of the form
Problem 1c
Posted: Sat Feb 12, 2005 4:32 pm
by asayers
I found the amplitude ratio and frequncies, and they weren't 1 and -1. So when I add the two modes in the solution, is it the first ratio times the a and the other ratio times the b constant?
Re: Problem 1c
Posted: Sun Feb 13, 2005 2:46 am
by goodwine
asayers wrote:I found the amplitude ratio and frequncies, and they weren't 1 and -1. So when I add the two modes in the solution, is it the first ratio times the a and the other ratio times the b constant?
I don't have my notes with me, but since the initial velocities are assumed to be zero, there are only two constants to specify. I don't remember the specific answers, but assume a1/a2=2 for one answer and a1/a2=3 for the other one. You can leave the coefficient for the solution for the first mass unspecified for each mode (and call the coefficients a and b) and then for the second mass the coefficients would just be 2a and 3b, respectively.
Caveat: since I don't have my notes with me, I can't say whether I used a and b in the above answer in the same way I did in class, but if you can follow what I said, you should be able to get the idea.
HW5
Posted: Mon Feb 14, 2005 7:40 pm
by harrier03
Sorry if this was supposed to be posted elsewhere. Regardless of when the homework is due, if it could be posted at the end of this week, like it normaly would, it would be nice. thanks
Re: HW5
Posted: Mon Feb 14, 2005 7:54 pm
by goodwine
harrier03 wrote:Sorry if this was supposed to be posted elsewhere. Regardless of when the homework is due, if it could be posted at the end of this week, like it normaly would, it would be nice. thanks
Nope, this is fine. I'll make it available on Friday at the latest.
Posted: Tue Feb 15, 2005 8:07 am
by mightyduck
Let's have the homework due Friday of next week instead of Wednesday of next week, please. Thanks!!
Homework 5 vote
Posted: Tue Feb 15, 2005 3:07 pm
by student
I agree with mightyduck. Have it due on a Friday instead of Wednesday.
HW # 5
Posted: Tue Feb 15, 2005 3:45 pm
by HugsyMcHugs
Due next wednesday as it normally would be.
Posted: Wed Feb 16, 2005 1:35 pm
by goodwine
Is it possible to give us a little guidance on where the material in the homework can be found in the text book? My notes alone seem to be not enough information to solve the homework problems. Perhaps the other students are encountering similar problems.
As I mentioned in class, the vibrations stuff is from Den Hartog. However, since that book isn't required, I made sure that I gave basically all the information in class.
If you came to all the classes, your notes are complete with regard to what you need to know for the material on repeated roots. The corresponding book section is the "Repeated Roots" one. However, apparently Boyce and Di Prima don't think that undergraduates are smart enough to handle repeated roots for the case where the matrix is bigger than 2x2. I disagree; hence, I did the full nxn case in class. You'll have to rely on your notes for this. It hasn't seemed to be a problem for classes in the past, so I expect that the notes will suffice.
frequency response
Posted: Thu Feb 17, 2005 6:18 pm
by Laplace
I am confused about the amplitude ratio.
Is it supposed to be -1 and 1? Hartog shows this is the case when k1 = k2, but he is using a system where k2 is actually a k3.
I did it out myself and got something other than -1 and 1.
For omega^2 I got + or - 1/(2^.5). I'll double check that later.
for a1/a2, after I substitute in for k and m equal 1 I get the ratio equals 1/(-w^2 + 2) or -w^2/1 +1. I'll check that later, but if I'm wrong on these let me know.
I'm not sure why we can pick 2 and 3.
Thanks
Re: frequency response
Posted: Thu Feb 17, 2005 10:16 pm
by goodwine
Laplace wrote:I am confused about the amplitude ratio.
Is it supposed to be -1 and 1? Hartog shows this is the case when k1 = k2, but he is using a system where k2 is actually a k3.
I did it out myself and got something other than -1 and 1.
The answer is not 1 and -1. If you think about it intuitively, in at least one mode the second mass should move more than the first one. There are kind of crazy analyitcal expressions for them. If I recall correctly, in decimals one is something like 1.6xxx (it may be -1.6xxx).
Laplace wrote:
For omega^2 I got + or - 1/(2^.5). I'll double check that later.
for a1/a2, after I substitute in for k and m equal 1 I get the ratio equals 1/(-w^2 + 2) or -w^2/1 +1. I'll check that later, but if I'm wrong on these let me know.
I'm not sure why we can pick 2 and 3.
Thanks
Again, I don't have my notes with me, but what you got for omega^2 does not look familiar. Your expressions for a1/a2 do look familiar.
I'm not sure what you mean by "pick 2 and 3."
[color=red]TYPO[/color]
Posted: Thu Feb 17, 2005 10:20 pm
by goodwine
The "i" in the exponent for the expression of the homogeneous solution for a vector in the null space of (A - lambda_i I )^m should be "lambda_i".
I fixed it, but I'm sure that by this time everyone has already printed the homework. Hopefully it hasn't caused any confusion. Since I haven't heard anything about it, I suppose it hasn't.
Sorry.
solutions
Posted: Mon Feb 21, 2005 5:08 pm
by Laplace
I cannot find the solutions, I assume they are not posted yet.
Could we get these as soon as possible? It would be beneficial for studying for the upcoming exam.
Re: solutions
Posted: Mon Feb 21, 2005 6:21 pm
by goodwine
Laplace wrote:I cannot find the solutions, I assume they are not posted yet.
Could we get these as soon as possible? It would be beneficial for studying for the upcoming exam.
Yes you may. Since I have such a lenient extension policy, some people actually just submitted the homework today, so there was no way that I could post it sooner. It will appear soon.
Posted: Tue Feb 22, 2005 4:29 pm
by Laplace
Thank you.
It would be good to get solutions for HW 2-5 before the test, the earlier the better. All I can find is 1. Old exams with solutions would be good also.
Posted: Tue Feb 22, 2005 4:53 pm
by goodwine
Laplace wrote:Thank you.
It would be good to get solutions for HW 2-5 before the test, the earlier the better. All I can find is 1. Old exams with solutions would be good also.
I just sent an email harassing the TA's for the solutions. I thought most of them were actually posted. I'll get them all up within a couple days, with the exception of the solutions for HW 5 which will be posted next Monday after class.
Posted: Wed Feb 23, 2005 11:17 pm
by Laplace
I would like to politely agree. This semester it is a lot more difficult because we have no solution tree and cannot reference the text. I have notes for each class, but sometimes it is hard to see where the notes apply. I am not saying that class is useless. I come to every class and try to get the most out of it.
I have found that typeset class handouts are very helpful such as the one for HW3. It would also be good if we could get a summary of what we have learned so far and where we can find it in our notes. Studying is a little harder this semester because we have so few examples, little book backup, and no solutions for the homework.
goodwine wrote:Is it possible to give us a little guidance on where the material in the homework can be found in the text book? My notes alone seem to be not enough information to solve the homework problems. Perhaps the other students are encountering similar problems.
As I mentioned in class, the vibrations stuff is from Den Hartog. However, since that book isn't required, I made sure that I gave basically all the information in class.
If you came to all the classes, your notes are complete with regard to what you need to know for the material on repeated roots. The corresponding book section is the "Repeated Roots" one. However, apparently Boyce and Di Prima don't think that undergraduates are smart enough to handle repeated roots for the case where the matrix is bigger than 2x2. I disagree; hence, I did the full nxn case in class. You'll have to rely on your notes for this. It hasn't seemed to be a problem for classes in the past, so I expect that the notes will suffice.
Posted: Thu Feb 24, 2005 8:00 am
by goodwine
Laplace wrote:I would like to politely agree. This semester it is a lot more difficult because we have no solution tree and cannot reference the text. I have notes for each class, but sometimes it is hard to see where the notes apply. I am not saying that class is useless. I come to every class and try to get the most out of it.
I have found that typeset class handouts are very helpful such as the one for HW3. It would also be good if we could get a summary of what we have learned so far and where we can find it in our notes. Studying is a little harder this semester because we have so few examples, little book backup, and no solutions for the homework.
Well, I hate to say it but you're probably going to have to get by with what's in the book, the solutions (I admit they've been late) and the notes. 90% of the material is actually in the book so a good starting point would be to work to reconcile your class notes with the book since you seem to see them more disconnected than they really are. What's not in the book is the vibrations stuff (which was really only a couple days) and the approach for repeated eigenvectors since the book treated it superficially. To the extent I can (office hours and/or a meeting with you) I'm happy to try to get it all together as much as possible.