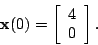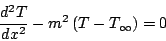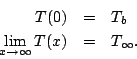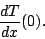Bill Goodwine's Courses

Unless otherwise indicated, all problems are from Elementary Differential Equations and Boundary Value Problems, by Boyce and DiPrima, 8th Edition.

1. Section 7.9 numbers 1 and 4 by
   1. diagonalization;
   2. undetermined coefficients; and,
   3. variation of parameters.
2. Section 7.9 number 3 by undetermined coefficients.
3. Section 7.9 number 5 by variation of parameters.
4. Section 7.9 number 7 by any method.
5. Using your general solution for Section 7.9 number 3, determine the solution if
   • 
6. Write and submit computer program (in C, C++ or FORTRAN) to determine a numerical approximation for the solution to the equation and initial condition in the previous problem. Compare the exact solution and the numerical approximate solution.
7. Determine T(x) that satisfies
   • 
   where
   • 
   Also determine
   • 

I'm having a problem solving for the coefficients in Problem 3. I assumed a particlar solution of the form x_p = a*t*cos(t) + b*t*sin(t) + c*cos(t) + d*sin(t) and I substituted into the equation, giving me eight equations and eight unknowns. However, I always get something uninformative like 0 = 0 or a = a when I try to solve for them. Any hints?

bprenger wrote:I'm having a problem solving for the coefficients in Problem 3. I assumed a particlar solution of the form x_p = a*t*cos(t) + b*t*sin(t) + c*cos(t) + d*sin(t) and I substituted into the equation, giving me eight equations and eight unknowns. However, I always get something uninformative like 0 = 0 or a = a when I try to solve for them. Any hints?

I don't have my book with me, so I can't work it out until tomorrow morning. Your assumed form of the particular solution looks o.k. (assuming this is the problem with the purely imaginary lambda-i eigenvalues). Did you check your algebra using a computer or calculator, or did you do it all by hand? If the latter, I'd guess (but not guarantee) a computational error.

Your approach is definitely o.k.

When I get a chance (hopefully sometime tomorrow) I'll post again. If you figure it out, please post as well, even if it's just an algebra error.

bprenger wrote:I'm having a problem solving for the coefficients in Problem 3. I assumed a particlar solution of the form x_p = a*t*cos(t) + b*t*sin(t) + c*cos(t) + d*sin(t) and I substituted into the equation, giving me eight equations and eight unknowns. However, I always get something uninformative like 0 = 0 or a = a when I try to solve for them. Any hints?

When you have to multiply the assumed form of the homogeneous solution by t and then add it to the homogeneous solution (like you did), there will generally be a nonunique solution, i.e., you may have 8 equations and 8 unknowns, but there may be an infinite number of solutions.

This happens because one of the terms in the particular solution is still just the same as the homogeneous solution; therefore, when you write down the general solution (homogeneous + particular) there are an infinite number of ways to combine one (or more) of the homogeneous solutions with a term in the particular solution.

Your 0=0 or a=a equations are simply a manifestation of nonuniqueness. Any solution of your 8 equations will be fine.

For the first problem I keep getting different answers for different approaches. Based on what was said above, does that mean that there are multiple (but similar) solutions to the same problem?

lisaturtle wrote:For the first problem I keep getting different answers for different approaches. Based on what was said above, does that mean that there are multiple (but similar) solutions to the same problem?

The solution is unique; however, since no initial conditions were specified, they answers may be the same and look different because of the different way that the coefficients in the general solution may be combined with the parts of the particular solution.

For example, in problem 1 in section 7.9, the answer in the back of the book has two terms with e^t. Forgetting the rest of the terms, the following are the same:

c1 (1,1) e^t - 1/4 (1,3) e^t

and

k1(1,1) e^t - 1/2 (0,1) e^t

because we can let k1 = c1-1/4.

The point is that the term that goes with the particular solution looks completely different, but the difference can be absorbed by the term in the homogeneous solution that is multiplied by a constant. So checking your answers with each other or with the back of the book is, unfortunately, sometimes difficult. I can't offer any suggestions other than to check to see whether there is a way to combine the terms to give the same answer.

The Kid wrote:n Problem 7.9 #5 we have repeated eigen values. I was just wondering if we just use the same eigen vectors that we calculated to make the matrix to start using variation of parameters (you denoted it with a capital greek letter) .

For the fundamental matrix you simply need a full set of n linearly independent homogeneous solutions (no matter how your obtain them). So, solve the homogeneous equation, including if necessary all the terms multiplied by t in the case of repeated roots and generalized eigenvectors, and put them together column by column in the fundamental matrix, Xi.

In problem 5 of section 7.9 I don't understand how to do the integration step of variation of parameters. Integrating from 0 to t gives an impossible answer with zeros in the denominators, so what do I use as a lower limit if I don't use 0?

dmahone1 wrote:In problem 5 of section 7.9 I don't understand how to do the integration step of variation of parameters. Integrating from 0 to t gives an impossible answer with zeros in the denominators, so what do I use as a lower limit if I don't use 0?

I'm at home and don't have my book with me so I can't check any details, but I strongly suspect you have a computational error. I'll get back to you tomorrow morning if no one else volunteers an explanation before then.

For Problem 1.a, I cannot get TAT^-1 to look like it should, i.e. a matrix of all zeroes with the eigenvalues on the diagonal. I have compared it to three other students, none of whom were able to either. We are using calculators so I don't think there's a mistake. Are we misunderstanding something? Is TAT^-1 really supposed to be equal to a matrix of all zeroes with the eigenvalues on the diagonal.

Also, when constructing T out of eigenvectors, should we normalize them first?

For Problem 1.b, I cannot get a working particular solution from the formulae provided. I can get a working particular solution from guessing... it is Ate^t + Be^t + Ct^2 + Dt + E, where A-E are vectors... but I have to intruduce the t^2 term (that multiplies C), which I don't think I should have to do. Questions:

(1) Is this allowable? It is, after all, still a particular soln.
(2) Is this the desired method, or is there a way the formulae will give a correct answer without guessing and checking.

monkeybrains wrote:For Problem 1.a, I cannot get TAT^-1 to look like it should, i.e. a matrix of all zeroes with the eigenvalues on the diagonal. I have compared it to three other students, none of whom were able to either. We are using calculators so I don't think there's a mistake. Are we misunderstanding something? Is TAT^-1 really supposed to be equal to a matrix of all zeroes with the eigenvalues on the diagonal.

I'm not sure if I ever wrote it incorrectly in class, but it should be T^(-1) A T, not T A T^(-1).

monkeybrains wrote:Also, when constructing T out of eigenvectors, should we normalize them first?

It doesn't matter whether or not you do. The effect of normalizing them is "undone" by the T^(-1) term, i.e., however they are scaled in T by normalization, they are effectively unscaled by T^(-1).

monkeybrains wrote:For Problem 1.b, I cannot get a working particular solution from the formulae provided. I can get a working particular solution from guessing... it is Ate^t + Be^t + Ct^2 + Dt + E, where A-E are vectors... but I have to intruduce the t^2 term (that multiplies C), which I don't think I should have to do. Questions:

(1) Is this allowable? It is, after all, still a particular soln.
(2) Is this the desired method, or is there a way the formulae will give a correct answer without guessing and checking.

Well, in life it's allowable since the point is to get the solution. When not in the real world, if I say on an exam to "find the solution," then it's o.k. If I say "find the solution using xxx method," unless the "xxx method" is the "guessing method" then it's not o.k.

Unless someone else pipes in, I'll have to get back to you since I don't have the book with me.

student wrote:For problem 3, I assumed x_p = a*t*cos(t) + b cos(t) + c**t*sin(t)+ d*sin(t), substituted, and equated coefficients. The equations I got are
a = -Ac
c = Aa
a+d = Ab -{{1},{0}}
-b+c = Ad +{{0},{1}} All are in vector form.
When I try to get a and c, I only get a bunch of 0=0's
Am I messing up the algebra or something earlier?

When you get equations like 0=0 or a=a, it means one of the variables is arbitrary.

Especially if your equation is like 4b = 4b, any b satisfies that equation, so you can generally pick b=0. When you get 0=0, look to see where it came from, and that will usually tell you which variable is arbitrary.

I'm confused when it comes to solving #7. How do I take into account t_infinity? Can I just treat it as a constant?

wgallag1 wrote:I'm confused when it comes to solving #7. How do I take into account t_infinity? Can I just treat it as a constant?

Yes, T is the dependent variable, x is the independent variable. T_\infty is a constant.