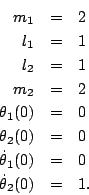Page 1 of 1
Homework 6, due Wednesday, March 16.
Posted: Fri Mar 04, 2005 8:05 pm
by goodwine
- Consider the double pendulum illustrated in the following figure. Note that the definition of the second angle is different than the example from class. Use Lagrange's equations to determine the equations of motion for the system.
- Let
Write a computer program to determine an approximate numerical solution to the equations of motion for the system with the given parameter values and initial conditions. The angle values are given in radians. You may use any computer programming language or environment that you want (C, C++, FORTRAN, Matlab, Mathematica, Maple, etc.). Submit a plot of the solution for both angles.
- Now consider the same system but with forces due to gravity applied to each mass, as illustrated in the following figure. Determine the equations of motion for this system.
- Write a computer program to determine an approximate numerical solution to the equations of motion for the system with the same parameter values an initial conditions as problem 2. Again you are free to choose your programming language. Submit plots showing the solution for both angles.
Posted: Tue Mar 08, 2005 9:55 pm
by pegasusherd
In one of the homeworks from last semester, you showed us how to solve second order equations in MATLAB using the ode45 function by splitting the second order equation into two first order equations. However, that was just with one variable i.e. xdoubledot, xdot, x, etc.
How would we go about solving the equations of motion in this homework in MATLAB with ode45 where there are two independent variables in the equations i.e. theta1doubledot, theta2doubledot, theta1dot, theta2dot, theta1, theta2, etc.
Thanks
Posted: Wed Mar 09, 2005 3:46 pm
by goodwine
pegasusherd wrote:In one of the homeworks from last semester, you showed us how to solve second order equations in MATLAB using the ode45 function by splitting the second order equation into two first order equations. However, that was just with one variable i.e. xdoubledot, xdot, x, etc.
How would we go about solving the equations of motion in this homework in MATLAB with ode45 where there are two independent variables in the equations i.e. theta1doubledot, theta2doubledot, theta1dot, theta2dot, theta1, theta2, etc.
Thanks
The only fundamental thing you need to change is, instead of having a list of two "right hand sides" of the ode's, you have four. Other than that, as I recall, it's exactly the same.
Posted: Wed Mar 09, 2005 3:51 pm
by goodwine
How do I compute a numerical solution when theta1_double_dot and theta2_double_dot both appear in each equation of motion?
You have two equations of motion, so you have to solve them for each second derivative term.
Posted: Wed Mar 09, 2005 4:12 pm
by goodwine
I had a question about problem 3 in Homework 6. My notes are written, Q = Sum(Fi(a) dot partial(ri/qi)). I assume that this means the force applied, F(a)=m1g, and that r1 should be derived with respect to theta1. I just wanted to make sure that since this force is only in the y direction, that the answer should consist only of one term, equalling m1g(l1sin(theta1)).
Also, I wanted to ask if m1 only should be involved in the theta1 force, and m2 only in the theta2 force, or if they needed to be combined.
You want to write the position of each mass, r_i as a function of the theta's. For mass one it happens to be the case that it only depends on theta_1. For mass 2, r_2 depends on both.
Simply write F^(a) as a vector for each mass and plug and chug. Note that each generalized force, Q_j, corresponds to a coordinate (in this case one of the theta's) so in general the F^(a)'s will get mixed up into each of the equations. However, in this particular problem, since r_1 does not depend on theta_2, the force on mass 1 should not enter into the theta_2 equation.
Posted: Wed Mar 09, 2005 6:03 pm
by mjesick
goodwine wrote:How do I compute a numerical solution when theta1_double_dot and theta2_double_dot both appear in each equation of motion?
You have two equations of motion, so you have to solve them for each second derivative term.
Am I correct in saying that this is going to be a huge mess (even with initial conditions)?
Posted: Thu Mar 10, 2005 1:38 am
by pegasusherd
Going from my previous MATLAB question... I just want to be sure I understand this:
For one equation of motion, I should solve it for both theta1doubledot and theta2doubledot. Putting it into MATLAB as you showed us in your previous ode45 example, I will then have 4 equations for that one equation of motion: two equations simply defining the first derivatives of the two angles, and two equations defining the second derivatives of the two angles?
I tried that and got the MATLAB function to run, but from what it's giving me, I doubt it's correct. For problem 2 with the first equation of motion, I'm getting a constant zero for theta1 and theta2 increasing from zero with a slope of 1. Is that even what we're supposed to be plotting i.e. for each equation of motion, the two theta angles versus time? Is what I'm getting for that first equation of motion wrong like I think it is?
Posted: Thu Mar 10, 2005 2:10 am
by pegasusherd
I just realized something I'm doing...
For some reason I thought I had to solve each equation of motion individually, but it just hit me that we're supposed to be solving the equations of motion simultaneously. So for MATLAB, with solving 2 equations of motion, am I then going to have 8 equations since I came up with 4 equations for one equation of motion?
Posted: Thu Mar 10, 2005 2:15 am
by pegasusherd
ohhhh.....
or maybe I only solve the first equation of motion for theta1doubledot and only solve the second equation of motion for theta2doubledot? So that would give me four equations...
Sorry for my big blob of posting...
Posted: Sat Mar 12, 2005 8:36 am
by goodwine
mjesick wrote:goodwine wrote:How do I compute a numerical solution when theta1_double_dot and theta2_double_dot both appear in each equation of motion?
You have two equations of motion, so you have to solve them for each second derivative term.
Am I correct in saying that this is going to be a huge mess (even with initial conditions)?
It shouldn't be too bad after you substitute the numerical values for the masses, etc. It would definitely be a huge mess if you left everything as a symbolic variable.
Posted: Sat Mar 12, 2005 8:39 am
by goodwine
pegasusherd wrote:ohhhh.....
or maybe I only solve the first equation of motion for theta1doubledot and only solve the second equation of motion for theta2doubledot? So that would give me four equations...
Yes. Two "double dot" equations which gives 4 equations when you convert them to a system of first order equations.
pegasusherd wrote:Sorry for my big blob of posting...
Actually, I think it's helpful for others going through exactly the same thought process.
Posted: Sun Mar 13, 2005 4:31 pm
by mightyduck
In order to convert my equations of motion into 4 first order ones, I designated x1 = theta1, x2 = theta1dot, x3 = theta2, x4 = theta2dot. When I actually write out the 4x1 matrix of equations, however, there's a double dot term in the second and fourth rows. What am I supposed to call that double dot term? Should I be adding in an x5 and x6 or what?
Posted: Sun Mar 13, 2005 5:24 pm
by goodwine
mightyduck wrote:In order to convert my equations of motion into 4 first order ones, I designated x1 = theta1, x2 = theta1dot, x3 = theta2, x4 = theta2dot. When I actually write out the 4x1 matrix of equations, however, there's a double dot term in the second and fourth rows. What am I supposed to call that double dot term? Should I be adding in an x5 and x6 or what?
No, there should only be 4 equations. I'm not sure I completely follow what you are asking. Your x1 through x4 are the right variables. Then you want to determine d/dt [x1,x2,x3,x4] so the first equation will just be
x1dot = x2
and the third will be
x3dot = x4
and the second and fourth equations will be
x2dot = "whatever theta1doubledot is"
and
x4dot = "whatever theta2doubledot is"
Problem2
Posted: Sun Mar 13, 2005 5:43 pm
by asayers
I plotted the theta's for the 1st problem and they are reasonable up till about t=2 seconds, but then they explode. I realize that there is no gravity but am not sure if I'm dividing by zero somewhere either, which would cause the theta to be off the charts. Should the plot be reasonable for a larger time period?
Posted: Sun Mar 13, 2005 6:33 pm
by mightyduck
goodwine wrote:mightyduck wrote:In order to convert my equations of motion into 4 first order ones, I designated x1 = theta1, x2 = theta1dot, x3 = theta2, x4 = theta2dot. When I actually write out the 4x1 matrix of equations, however, there's a double dot term in the second and fourth rows. What am I supposed to call that double dot term? Should I be adding in an x5 and x6 or what?
No, there should only be 4 equations. I'm not sure I completely follow what you are asking. Your x1 through x4 are the right variables. Then you want to determine d/dt [x1,x2,x3,x4] so the first equation will just be
x1dot = x2
and the third will be
x3dot = x4
and the second and fourth equations will be
x2dot = "whatever theta1doubledot is"
and
x4dot = "whatever theta2doubledot is"
I understand all that, but the x2dot and x4dot equations contain thetadoubledots as well (i.e. x2dot contains a theta2doubledot). What am I supposed to call that theta2doubledot??
Posted: Sun Mar 13, 2005 6:35 pm
by smanwari
I'm having the same problem/confusion. When I solve the first equation of motion for theta1doubledot, on the right hand side of the equation is theta1,theta2, theta1dot, theta2dot, and theta2doubledot. Similarly when I solve the second equation of motion for theta2doubledot, the right has theta1doubledot along with everything else. I'm not really sure how to program this. When we are programming the Euler code for the theta1dot and theta2dot equations, what do we put in for the extra doubledot terms on the right hand side of the equation?
Posted: Sun Mar 13, 2005 7:02 pm
by goodwine
smanwari wrote:I'm having the same problem/confusion. When I solve the first equation of motion for theta1doubledot, on the right hand side of the equation is theta1,theta2, theta1dot, theta2dot, and theta2doubledot. Similarly when I solve the second equation of motion for theta2doubledot, the right has theta1doubledot along with everything else. I'm not really sure how to program this. When we are programming the Euler code for the theta1dot and theta2dot equations, what do we put in for the extra doubledot terms on the right hand side of the equation?
Think of them as two equations with two unknowns: the double dot terms. You have to solve the two equations for the acceleration terms.
Posted: Sun Mar 13, 2005 7:02 pm
by goodwine
mightyduck wrote:
I understand all that, but the x2dot and x4dot equations contain thetadoubledots as well (i.e. x2dot contains a theta2doubledot). What am I supposed to call that theta2doubledot??
See the post right above this one.
Animation
Posted: Tue Mar 15, 2005 1:57 am
by Grendel
Can you post the animation for the 2 mass, 2 spring, 2 damper system so that i can try to make the animation based off that?
Re: Animation
Posted: Tue Mar 15, 2005 7:52 am
by goodwine
Grendel wrote:Can you post the animation for the 2 mass, 2 spring, 2 damper system so that i can try to make the animation based off that?
For two reasons I don't think I'll do so.
- I think it's actually easier to do in Matlab and I did tit in Mathematica, and for most (not all) of you guys, Matlab skills are probably more important for your subsequent professional careers.
- I decided to give the 40 points extra credit (double for the whole homework) based upon you not having it. I would have given somewhat less if you had mine to work from. I'm sure if you spend a while with google you can find a good tutorial that will get you started.
Posted: Wed Mar 16, 2005 1:51 am
by Laplace
I just want to make sure of something. for (matrix r-derivativedot) dot (matrix r-derivativedot) we take the dot product of the top terms, and add to the dot product of the bottom terms? This leaves a scalar. Is this the same thing as the "inner product" of two matrices in linear algebra denoted <a,b>?
Posted: Wed Mar 16, 2005 10:59 am
by goodwine
Laplace wrote:I just want to make sure of something. for (matrix r-derivativedot) dot (matrix r-derivativedot) we take the dot product of the top terms, and add to the dot product of the bottom terms? This leaves a scalar. Is this the same thing as the "inner product" of two matrices in linear algebra denoted <a,b>?
It's just the usual dot product between two vectors. The dot product is an inner product, but an inner product is more general than just dot products.