Bill Goodwine's Courses

(20 points each) Determine the equations of motion for each of the systems illustrated in the following figures. For each system, clearly label your coordinates on the figure. If a parameter is missing that is necessary for the problem, feel free to add an appropriate label, but clearly indicate that you did so on the figure.

1. The following system is comprised of two masses and two springs. The first mass is constrained to move horizontally and the second mass is constrained to maintain contact with the angled surface of the first mass. It may be advisable, although not necessary, to use the horizontal deflection of the first mass from the unstretched position of spring one as the first coordinate and the deflection of mass 2 along the surface of mass one from the unstretched position of spring 2 as the second coordinate for this problem.
   • 
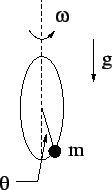
2. The following system is comprised of a circular wire hoop that rotates about its vertical axis with a constant angular velocity of $\omega$. A particle or bead is constrained to slide along the hoop, and $\theta$ is the angle of the bead from the ``straight down'' position. Hint: you only need to consider the motion of the particle - since the hoop moves with a constant angular velocity, it does not really have any ``dynamics.''
   • 
3. The following system is a double pendulum. The only difference between this one and the example in class is that there is a torque about each hinge. The first hinge has a torque of $\tau = \sin t$ and the second hinge has a torque of $\tau = \sin 2 t$. Assume that each link is massless.
   • 
4. This system is a turntable with moment of inertia $I$. Its angular position is represented by the coordinate $\theta$. On the surface of the turntable there is a groove or slot oriented radially along which a mass of mass $m$ is constrained to move. The mass is attached to a spring with spring constat $k$. The coordinate $x$ represents the radial position of the mass and is measured from the unstretched position of the spring.
   • 
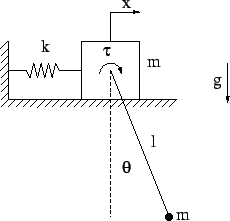
5. This system is a mass-pendulum system like the example considered in class on March 5. The only difference is that there is a torque, $\tau = \cos t$ applied at the hinge of the pendulum. Assume the link is massless.
   • 

Classmates:

My assignment for HW 5 (the one that was due right before Exam I) disappeared from the Fitz Cluster the day before it was due; all my other stuff was there but the folder it was in was gone... It hasn't turned up, and it was a long assignment so I figured maybe someone needed the assignment and took it.

My heat transfer test and some other papers which I need were also in that folder. I don't care about the assignment, but if you have the folder, just put it back in Goodwine's returned homework pile. This would help me out a lot. Thank you.

It says to essentially ignore the dynamics of the hoop and treat this as a one body system. I'm confused though on how to to treat the angular velocity. Do we take it into account in the kinetic energy of the mass and just treat the mass as having an angular velocity as well it's rdot dot rdot term?

asayers wrote:It says to essentially ignore the dynamics of the hoop and treat this as a one body system. I'm confused though on how to to treat the angular velocity. Do we take it into account in the kinetic energy of the mass and just treat the mass as having an angular velocity as well it's rdot dot rdot term?

The only "body" or "particle" is the mass that goes around the hoop. The hoop just constrains the motion of the particle. However, the velocity of the particle will depend on omega, so omega will show up on the kinetic energy of the particle.

Slightly confused about number 4. Is this another system where we only take the mass attached to the spring into account, or do we do something with the disk it's rotating on as well? How does the moment of inertia come into play (especially with respect to the mass)? A little shove in the right direction would be greatly appreciated!

mightyduck wrote:Slightly confused about number 4. Is this another system where we only take the mass attached to the spring into account, or do we do something with the disk it's rotating on as well? How does the moment of inertia come into play (especially with respect to the mass)? A little shove in the right direction would be greatly appreciated!

There is an important distinction between problems 2 and 4 which you currectly recognize. In problem 2 the hoop is constrained to rotate at an angular velocity omega. In this problem, the disk has an inertia and will not (necessarily) rotate with a constant angular velocity. So the two bodies in this problem are the disk and the other mass. So there are two degrees of freedom and two coordinates. Simply compute kinetic and potential energies and plug and chug.

Can we neglect gravity forces for number 4?

mightyduck wrote:Can we neglect gravity forces for number 4?

Yes, there is no gravity in number 4.

on these two problems, do we have to do x, y, and z coordinates? i think we do for number 2 but im not sure for number 3. and on number two, i ran into trouble when i had an equation for T in two coordinates but when i went to derive Q i had only one force vector to work with, so i had nothing to dot the partial of T with respect to the second coordinate, omega.

Thanks.

this is fun to look at:

acrutchf wrote:on these two problems, do we have to do x, y, and z coordinates? i think we do for number 2 but im not sure for number 3. and on number two, i ran into trouble when i had an equation for T in two coordinates but when i went to derive Q i had only one force vector to work with, so i had nothing to dot the partial of T with respect to the second coordinate, omega.

Thanks.

this is fun to look at:

In order to compute the kinetic energy of the mass in problem 2, you need to compute (x,y,z) but they will only be a function of one coordinate, theta. The constant omega will appear in it as well, but since it doesn't change, it's not a coordinate. The hoop problem has only 1 coordinate and equation.

For problem 3, it's just like the example problem from class in terms of the kinetic energy, etc. The only difference is the applied torques.

I don't think that Problem 4 should be as neat and easy as I found it to be. Could you give me a start for T and V?

student wrote:I don't think that Problem 4 should be as neat and easy as I found it to be. Could you give me a start for T and V?

V is just from the sprng.

T is the sum of the kinetic energies of the disk and mass. The disk is just 1/2 I thetadot^2. The mass is harder, but is 1/2 m times the sum of the squares of the radial and tangential velocities.