Bill Goodwine's Courses

You will need to wait until after class on Wednesday or Friday to complete problems 3 and 4. The example during the first half of Wednesday's class will be helpful, but not necessary, to compete the first two problems.

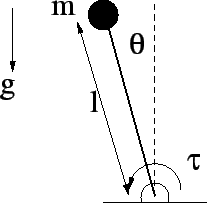
1. Consider the inverted pendulum illustrated in the following figure (you may consider the mass to be an idealized point mass).
   • 
   1. (5 points) Determine the equation of motion for the system and then determine the linear approximation to the system by assuming that the angle is small so that you may assume that sin(theta) is approximately theta and cos(theta) is approximately 1.
   2. (5 points) Determine the transfer function from the input torque to the output angle.
   3. (5 points) Determine the transfer function from the input torque to the output angular velocity.
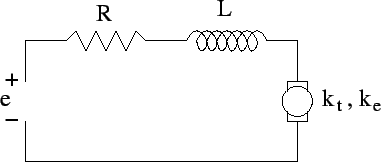
   4. Assume the torque is supplied by a d.c. motor, as illustrated in the following figure.
      • 
      • (5 points) Determine the transfer function from the applied voltage to the output angle.
      • (5 points) Determine the transfer function from the applied voltage to the output angular velocity.
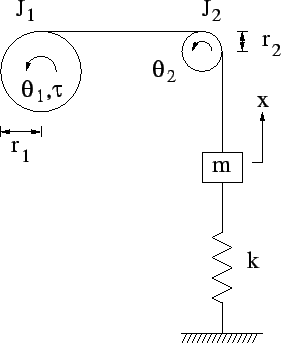
2. Consider the mass-pulley system illustrated in the following figure (assume the system is planar, i.e., no gravity).
   • 
   1. (5 points) Determine the equation of motion for the system. Hint: in addition to using Newton's law on the mass and two pulleys, assume that the cord does not slip on the cable. That assumption will provide two equations: one relating the angle of pulley 1, the radius of pulley 1, the angle of pulley 2 and the radius of pulley 2 and another relating the angle and radius of pulley two and the displacement of the mass (these are known as kinematic constraints).
   2. (5 points) Determine the transfer function from the torque to the position of the mass.
   3. (5 points) Determine the transfer function from the torque to the velocity of the mass.
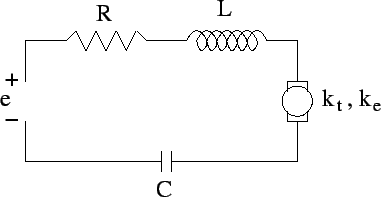
   4. Assume the torque is supplied by a d.c. motor, as illustrated in the following figure.
      • 
      • (5 points) Determine the transfer function from the applied voltage to the position of the mass. Hint: you may want to (perhaps even need to) add a variable for the voltage drop across the capacitor and then add an equation relating the current through the capacitor to the voltage across it.
      • (5 points) Determine the transfer function from the applied voltage to the velocity of the mass.
      • (5 points) Determine the transfer function from the current in the circuit to the position of the mass.
      • (5 points) Determine the transfer function from the current in the circuit to the velocity of the mass.
3. Find the transfer function Y(s)/R(s) for the following block diagram.
   • 
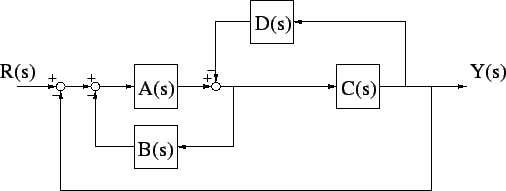
4. Find the transfer function Y(s)/R(s) for the following block diagram.
   • 

For problem 2, am I correct in that the sum of torques for pulley 2 is zero? This results in theta2 doubledot being zero, which essentially removes theta2 and r2 from the problem, which doesnt seem right. Am i missing something?

smanwari wrote:For problem 2, am I correct in that the sum of torques for pulley 2 is zero? This results in theta2 doubledot being zero, which essentially removes theta2 and r2 from the problem, which doesnt seem right. Am i missing something?

No, the sum of the torques on pulley two will not be zero. If there is any acceleration of the mass and pulley one, then pulley two must accelerate as well. The tension or force in the cables on either side of pulley two will not be the same, in general.

Should we be using Lagrange's eqns to find the equations of motion for each system? I'm not clear on how we should be finding these without having the circuit included too.

mightyduck wrote:Should we be using Lagrange's eqns to find the equations of motion for each system? I'm not clear on how we should be finding these without having the circuit included too.

You may, but I would personally use Newton's laws since the mechanical component of each system is pretty simple.

When you find the transfer function relating current and position/velocity, do you just use the equation of motion from part a with the substitution torque=k_t*i(t)? Don't you need to account for the circuit components somehow?

lisaturtle wrote:When you find the transfer function relating current and position/velocity, do you just use the equation of motion from part a with the substitution torque=k_t*i(t)? Don't you need to account for the circuit components somehow?

For the transfer function with the current, it's as simple as you indicated. Voltage to position will require the other circuit components.

When you say use assume the cord doesn't slip because it will then relate the angle and radius of pulley 2 to the displacement of the mass, do you mean pulley one? Because it looks like the cord will coil around pulley 1 and not pulley 2.

NDChevy07 wrote:When you say use assume the cord doesn't slip because it will then relate the angle and radius of pulley 2 to the displacement of the mass, do you mean pulley one? Because it looks like the cord will coil around pulley 1 and not pulley 2.

No. Actually, assuming the cord doesn't slip relates the angels of both pulleys to the displacement of the mass.

For the transfer functions in #1, do I use the regular equations of motion or the linear approximation?

student wrote:For the transfer functions in #1, do I use the regular equations of motion or the linear approximation?

It is only possible to use the linearized equations. The Laplace transform isn't defined for nonlinear functions of anything other than time.

In one example from class, there was a frictional torque on the motor. Is this a standard assumption for all electric motors, or was this parameter unique to the example problem?

drowinsk wrote:In one example from class, there was a frictional torque on the motor. Is this a standard assumption for all electric motors, or was this parameter unique to the example problem?

Don't assume any frictional damping term on a motor unless it is explicitly specified.