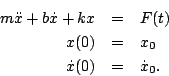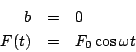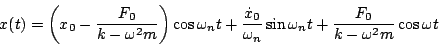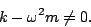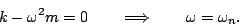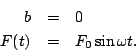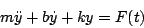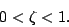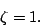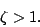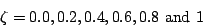Bill Goodwine's Courses

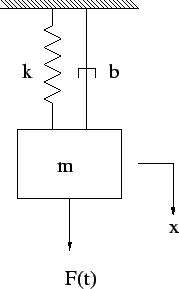
We love the system illustrated in the following figure so much that we are going to solve every reasonable permutation of it. The reason we love it so much is, of course, that it is so broadly applicable to many important engineering problems that entire text books are devoted to it.

• • 

Unless otherwise indicated, assume there is no gravity and that x is measured from the unstretched position of the spring. In this case, the equations of motion are

• • 

1. For the case where
   • 
   we showed in class that
   • 
   as long as
   • 
   1. Determine the solution in the case where
      • 
   2. Plot the solution. A hand sketch is adequate as long as it is qualitatively accurate.
   3. When the forcing frequency is very close, but not exactly equal, to the natural frequency which solution (the solution you just determined or the one from class) is correct? Plot the solution. Again, a hand sketch is adequate as long as it is qualitatively accurate.
2. Determine the solution when
   • 
   Indicate whether it matters if
   • 
   If it does matter, then you may assume that the inequality is true.
3. Assume for this problem that there is gravity.
   1. Derive the equations of motion when x is measured from the unstretched position of the spring.
   2. Show that the equation of motion for the system is
      • 
      when y is measured from the static equilibrium of the system, i.e., under gravity the weight of the mass would stretch the spring by an amount x=mg/k so y=x-mg/k.
   The significance of this is that even if there is gravity, we can neglect is as long as the position of the mass is measured from the position of static deflection of the spring due to the weight of the mass.
4. For damped unforced (F(t)=0) oscillations, we showed in class that the (homogeneous) solution to the equation given at the top of the page is
   • 
   as long as
   • 
   1. Determine the (homogeneous) solution when
      • 
   2. Determine the (homogeneous) solution when
      • 
5. For the damped unforced oscillation case where
   • 
   plot the solution for
   • 
   for the time interval t=0 to t=10. Plot all the curves on the same plot.