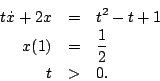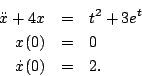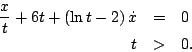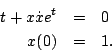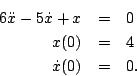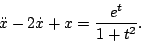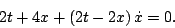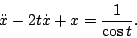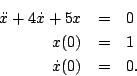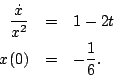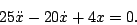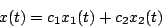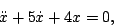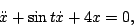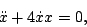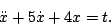Homework 2, due September 8, 2006.

[goodwine]

1. For each of the equations from problem 5 in homework 1 determine which, if any, of the following solution methods apply:
   1. the method of integrating factors from section 2.1
   2. the method for separable equations from section 2.2
   3. the method for exact equations from section 2.6
   4. assuming exponential solutions
   5. undetermined coefficients from section 3.6
   6. variation of parameters from section 3.7
   7. none of the above.
   Note: in some cases more than one method will apply, in which case you need to only specify any one of the methods for an answer. Any method that will work is a correct answer but it's probably worth considering which method would be the easiest to use.
   
   For problems 2 through 12 find the solutions indicated. If the equation cannot be solved using a method from chapters 2 or 3 in the course text, the correct answer is to indicate that the equation cannot be solved using the methods from the course text.
2. Determine the solution to
   • 
3. Determine the solution to
   • 
4. Determine the general solution to
   • 
5. Determine the solution to
   • 
6. Determine the solution to
   • 
7. Determine the general solution to
   • 
8. Determine the general solution to
   • 
9. Determine the general solution to
   • 
10. Determine the solution to
    • 
11. Determine the solution to
    • 
12. Determine the general solution to
    • 
13. Assume that x1(t) and x2(t) are solutions to the following ordinary, second order differential equations. For which of the following is the linear combination of the two solutions
    • 
    also a solution?
    1. 
    2. 
    3. 
    4. 
    What are the differences between the cases where the linear combination is a solution and the cases where it is not?

[goodwine]

Someone asked me:

I have a question on the first question on our homework due tomorrow. I was wondering if assuming exponential solutions means using the characteristic formula and substuting in r and factoring etc. Thanks for the help.

Asking yourself and then answering the question "where does the characteristic equation come from?" effectively answers this question for you.