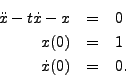Page 1 of 1
Homework 4, due October 4, 2006.
Posted: Wed Sep 27, 2006 4:55 pm
by goodwine
Do problems 1, 5 and 13 from the exercises in Chapter 4 of the course text.
Plot several partial sums in a series solution about
t=0 to
Example 4.3
Posted: Mon Oct 02, 2006 5:05 pm
by rross
I am having some trouble with a step made in example 4.3. I am sure it isn't as hard I as I am thinking about it but I can't see it so if someone knows what is going on, could you help clarify this for me.
The step in question is in the grouping of the X^n+r-1 terms. Where does the (2n+2r-1) term come from?
Thanks
Retracting Previous Statement
Posted: Mon Oct 02, 2006 11:19 pm
by rross
I spent some time with it again tonight and I am good, so no need for reply.
Some hints
Posted: Thu Oct 05, 2006 8:38 am
by goodwine
- Problems 1 and the last one are series solutions. Problem 5 is the easiset. Both of the equations in problem one are singular. The first one is straight-forward, but algebraically very messy. Perhaps using Mathematica may make doing it faster. When I did the second one, I got the unusual case whith r=0 was repeated. Just following the procedure for the repeated r case seems to work.
- Problem 5 (pendulum). There is some ambiguity that I should have caught eariler, so I apologize for not taking care of this before now. I'll explain the way I want it done, but there are alternative correct ways to do this problem. If you didn't do it exactly the way I recommend, but basically did it correctly, then you don't need to change your work.
Expand the sin(x) term out to third order. Just like in class, treat the 1/6 as a small parameter multiplying the nonlinearity. You may call it epsilon if you want, but recognize that there is another epsilon in the problem, and there is no reason that the other epsilon will be equal to 1/6! Do the perturbation just like in class for the 1/6 epsilon. The initial condition will not appear in the order 0 equaion, but rather in the O(1) one. Then use strained coordinates. If doing so doesn't change anything, then explain why it doesn't do anything (the answer is pretty straight-forward!).
- As I said in class, you should do an expansion for cosh(epsilon) up to third order and then follow the regular procedure for the perturbation. Epsilon will show up in, I believe, the initial condition for the second order equation. If you already did the problem using cosh(epsilon) as the initial condition for the first order equation only, do it again (it won't take too long) with the expansion and compare your two answers. Did it make any difference to put all the initial condition in the O(0) equation versus expanding the cosh?
prob 1b
Posted: Thu Oct 05, 2006 5:10 pm
by PatBowles
Several of us worked out problem 1b and did not get a repeated root, instead we found roots of 0, and -1 and must follow the third solution set when r1-r2 is a positive integer. This gets pretty messy! We later found k=0. If you forget to multiply by two in front of the second term in the differential equation, you end up with repeated roots.