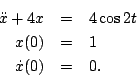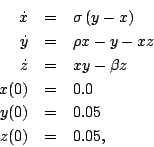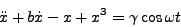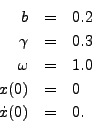- Consider
- Determine the analytical solution.
- Convert this second order equation into two first order equations.
- Write a computer program that uses the 4th order Runge-Kutta method to compute an approximate solution for the time interval t=0 to t=10. Determine a good time step by comparing the approximate solution to the analytical solution. Submit a plot of the solution.
- Plot the solution on the phase plane which is a plot of x(t) on the abscissa and dx/dt on the ordinate. The course text has a discussion of the phase plane as does the course notes that I wrote. Googling "phase plane" gives plenty of descriptive links as well.
- Consider the famous Lorenz equations
- Using 4th order Runge-Kutta determine an approximate numerical solution to these equations for the time range t=0 to t=50. Submit a 3D plot of (x,y,z). Be sure to experiment with the time step to ensure that your solution is accurate. The Matlab plot3() function will probably be useful. A quick google search will probably give you an idea of what the plot should look like.
- Use Matlab's ode45() to compute an approximate solution and plot the result.
- (5 points extra credit) Explain the significance of these equations.
- Consider
- Plot x(t) versus t.
- Plot the solution on the phase plane.
- (5 points extra credit) What is the name of this equation?
Homework 9, due November 8.
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Homework 9, due November 8.
Bill Goodwine, 376 Fitzpatrick
-
awulz
Poll Question - Choice 5
Here is what Choice 5 equates to: (Computed in Matlab)
2 Exams worth 18.5914% each
Final worth 42.8172%
Homework worth 20%
Someone please confirm. Thanks
Alex

2 Exams worth 18.5914% each
Final worth 42.8172%
Homework worth 20%
Someone please confirm. Thanks
Alex
-
mattstorey