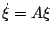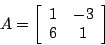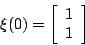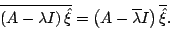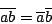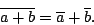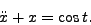Homework 3, due February 7, 2007.

[goodwine]

Unless otherwise indicated, all problems are from the course text, Elementary Differential Equations and Boundary Value Problems, by Boyce and DiPrima, 8th Edition.

1. Section 7.6, numbers 2, 4, 7, 8 and 10.
2. Solve
   • 
   where
   • 
   and
   • 
   1. by using one eigenvalue/eigenvector pair and the u(t) and v(t) approach as recommended in class and in the book; and,
   2. by computing both eigenvalue/eigenvector pairs and directly computing
      • 
3. To prove that eigenvectors associated with a complex conjugate pair of eigenvalues are also complex conjugates, in class I made use of the fact that if the matrix A is real then
   • 
   In order to justify this, it must be true that the complex conjugate of the product of two numbers is the product of the complex conjugates, i.e.,
   • 
   and
   • 
   Prove both of these facts.
4. Determine the general solution to
   • 

[tshinnic]

im trying to simplify the complex solutions and get rid of the i. I'm following the book and I see that you split the imaginary and real solutions of x1 up and add them together. What confuses me is that the imaginary and real part of the solution, u and v, only cover x1. x2 has an opposite value for w, (cos(wt) +isin(wt)) so different u and v values. The general solution is x = x1 + x2, and I dont see how that = c1U + c2V.

So what Im asking is how does:
(im leaving out the coefficients to make it easier to read)
x1 = u1 + v1
x2 = u2 + v2
X = x1 + x2
X =! u1 + v1 + u2 + v2 ?
the book just writes that x = u + v and says u and v are lin independant. I dont see how that completes the solution.

[goodwine]

im trying to simplify the complex solutions and get rid of the i. I'm following the book and I see that you split the imaginary and real solutions of x1 up and add them together. What confuses me is that the imaginary and real part of the solution, u and v, only cover x1. x2 has an opposite value for w, (cos(wt) +isin(wt)) so different u and v values. The general solution is x = x1 + x2, and I dont see how that = c1U + c2V.

What the book does is basically assert that the real and imaginary parts of one of the solutions may be taken as two linearly independent solutions. Then they just say (without any derivation or proof -- they have it in exercise 27) that they are linearly independent. However, they are linearly independent. One way to think about it is that the two eigenvalues and eigenvectors are very closely related (complex conjugates), so it isn't surprising that you can construct both solutions from one of them.

In class I took both solutions and then combined them to get the u and v solutions.

As a purely problem solving matter, what you want to do is just compute the eigenvalue and eigenvector, determine their real and imaginary parts, and then plug the result into equation 9 in the book (or the same one I derived in class).

So what Im asking is how does:
(im leaving out the coefficients to make it easier to read)
x1 = u1 + v1
x2 = u2 + v2
X = x1 + x2
X =! u1 + v1 + u2 + v2 ?
the book just writes that x = u + v and says u and v are lin independant. I dont see how that completes the solution.

Those four steps are basically what I did in class (if I am correctly following what you are trying to say). I think your confusion happens when trying to combine the components that came from real and imaginary parts and then trying to reconstruct the original without putting i back in there.

[Euler]

Having a solution with imaginary numbers in it does not bother me.

Using Euler's relation to convert to sines and cosines is fine, and makes sense.

But it still bothers me that only x^(1) or x^(2) is needed after expanding out the complex exponentials. I'll have to look that over more.

Sometimes the book is hard to follow. Often the book is hard to follow. Equation 10 does not make much sense to me. I can see how u(t) and v(t) are obtained from x^(1) (putting aside x^(2) as redundant for A=real numbers), but then why is kasee^(3) not kasee^(1)? Where are they getting the kasee^(3)?

[Euler]

kasee-1 and kasee-2 are complex eigenvectors, whereas kasee-3, 4, etc may be more eigenvectors (>2x2?) which are purely real?

[goodwine]

Having a solution with imaginary numbers in it does not bother me.

Using Euler's relation to convert to sines and cosines is fine, and makes sense.

But it still bothers me that only x^(1) or x^(2) is needed after expanding out the complex exponentials. I'll have to look that over more.

Well, since \xi^1 and \xi^2 are complex conjugates, is there really any new information in the second one? If not, then it should make some sense that you only need one.

Sometimes the book is hard to follow. Often the book is hard to follow. Equation 10 does not make much sense to me. I can see how u(t) and v(t) are obtained from x^(1) (putting aside x^(2) as redundant for A=real numbers), but then why is kasee^(3) not kasee^(1)? Where are they getting the kasee^(3)?

I don't have the book with me now. I'll get back to this later this morning.

[Dayu]

Sometimes the book is hard to follow. Often the book is hard to follow. Equation 10 does not make much sense to me. I can see how u(t) and v(t) are obtained from x^(1) (putting aside x^(2) as redundant for A=real numbers), but then why is kasee^(3) not kasee^(1)? Where are they getting the kasee^(3)?

kasee^(3), kasee^(4), ..., kasee^(n) are the eigenvectors corresponding to the other real and distinct eigenvalues.
The general solution is combining all of the situations.