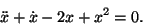Bill Goodwine's Courses

Consider

• 

1. Write this second order equation as a system of two first order equations.
2. Determine all the equilibrium points for this system.
3. By computing a Taylor series approximation to the nonlinear term, determine a linear approximation to the nonlinear system near each equilibrium point. This should be in the form of one second order differential equation.
4. Solve each linear approximation near each equilibrium point.
5. Plot the solution to the nonlinear equation (determined numerically using any method/program you choose) and the solution to the linear approximation for various initial conditions on the same phase plane to verify that the linear approximation is only valid near the equilibrium point. By inspecting the graph, provide an estimate of the region in which the linear approximation is valid.
6. By computing the Jacobian, determine the linear approximation to the system of two first order equations near each equilibrium point. This should be in the form of two first order differential equations.
7. By computing the eigenvalues and eigenvectors of the Jacobian matrix evaluated at the equilibrium point, determine the solution to the linear approximation.
8. If any of the fixed points have real eigenvalues, plot the corresponding eigenvectors on the phase plane plot. Explain what they represent.

to find the equilibrium points do you neglect the non-linear portion of the equation?

tscherbe wrote:to find the equilibrium points do you neglect the non-linear portion of the equation?

No, if you do that the only equilibrium will be the origin. You need to use the whole nonlinear equation to find the equilibria, then determine the best linear approximation near each one.

Two of us are having issues solving for the approximate solution for the second equilibrium point. When we compare our graphs, our approximate solution is perpendicular to the exact solution. We both solved this independently of each other and came to the same results. We were wondering if this is supposed to happen or if we're both doing something wrong.

clegault wrote:Two of us are having issues solving for the approximate solution for the second equilibrium point. When we compare our graphs, our approximate solution is perpendicular to the exact solution. We both solved this independently of each other and came to the same results. We were wondering if this is supposed to happen or if we're both doing something wrong.

Near the equilibrium point the solutions should be approximately the same, so there is an error somewhere. Without more information, though, I don't think I can be of much help.