Homework 6, due March 7, 2007.

Post by **goodwine** » Fri Mar 02, 2007 1:35 pm

Section 6.1, problems 1, 3 and 7.
Section 6.2, problems 11, 15 and 22.
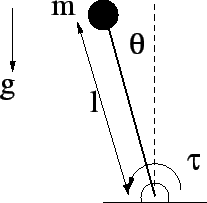
Consider the inverted pendulum illustrated in the following figure (you may consider the mass to be an idealized point mass).
1. (5 points) Determine the equation of motion for the system and then determine the linear approximation to the system by assuming that the angle is small so that you may assume that sin(theta) is approximately theta and cos(theta) is approximately 1.
2. (5 points) Determine the transfer function from the input torque to the output angle.
3. (5 points) Determine the transfer function from the input torque to the output angular velocity.
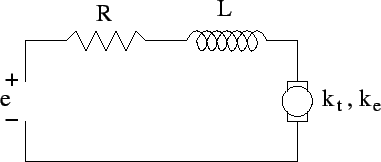
4. Assume the torque is supplied by a d.c. motor, as illustrated in the following figure.
  - (5 points) Determine the transfer function from the applied voltage to the output angle.
  - (5 points) Determine the transfer function from the applied voltage to the output angular velocity.
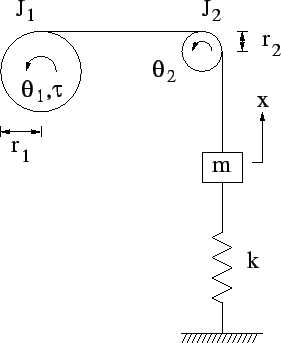
Consider the mass-pulley system illustrated in the following figure (assume the system is planar, i.e., no gravity).
1. (5 points) Determine the equation of motion for the system. Hint: in addition to using Newton's law on the mass and two pulleys, assume that the cord does not slip on the cable. That assumption will provide two equations: one relating the angle of pulley 1, the radius of pulley 1, the angle of pulley 2 and the radius of pulley 2 and another relating the angle and radius of pulley two and the displacement of the mass (these are known as kinematic constraints).
2. (5 points) Determine the transfer function from the torque to the position of the mass.
3. (5 points) Determine the transfer function from the torque to the velocity of the mass.
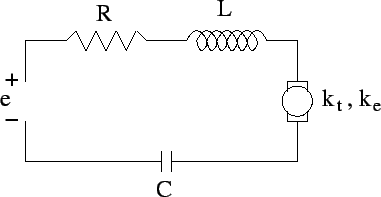
4. Assume the torque is supplied by a d.c. motor, as illustrated in the following figure.
  - (5 points) Determine the transfer function from the applied voltage to the position of the mass. Hint: you may want to (perhaps even need to) add a variable for the voltage drop across the capacitor and then add an equation relating the current through the capacitor to the voltage across it.
  - (5 points) Determine the transfer function from the applied voltage to the velocity of the mass.
  - (5 points) Determine the transfer function from the current in the circuit to the position of the mass.
  - (5 points) Determine the transfer function from the current in the circuit to the velocity of the mass.

mattstorey · Post by **mattstorey** » Mon Mar 05, 2007 3:16 am

are we to assume that the initial conditions for number 3 are 0

Post by **goodwine** » Mon Mar 05, 2007 6:50 am

mattstorey wrote:are we to assume that the initial conditions for number 3 are 0

Yes, whenever you are asked to find a transfer function assume that the initial conditions are zero.

Post by **goodwine** » Mon Mar 05, 2007 6:33 pm

In problem 22 I did the following:

After Laplace transforming everything I got something like

Y(s) = 1/(s^2 - 2s + 2) x (s+2)/(s+1)

where the "x" is times.

Completing the square gives

Y(s) = 1/[(s-1)^2+1] x (s+2)/(s+1)

Don't multiply the denominators together. Computing a partial fraction expansion like

Y(s) = (a s + b)/[(s-1)^2 + 1] + c/(s+1)

is what you need. Just cross multiply and equate numerators to find a, b and c (they are something like -1/5, 8/5 and 1/5 respectively). So we have

Y(s) = [(-1/5)s + 8/5]/[(s-1)^2 + 1] + (1/5)/(s+1).

The numerator of the first term isn't of the form of what's in the table (we want it to be (s-1)). So, factor out the -1/5, which will give a numerator of (s- 8 ). That's still not (s-1), but we can write

(s- 8 )/[(s-1)^2 + 1] = (s-1)/[(s-1)^2 + 1] - 7{1/[(s-1)^2 + 1]}

both of which are in the tables.

jgates1 · Post by **jgates1** » Tue Mar 06, 2007 12:06 am

I am having problems coming up with the equations of motion for problems 3 and 4. It has been a while since dynamics. Could you give a pointer on where to go with these questions so that I can do the rest of each problem?

mattstorey · Post by **mattstorey** » Tue Mar 06, 2007 12:23 am

can you tell me what im doing wrong on number 4, are we supposed to get an equation of torque in terms of x and its derivative for part a and if so how does theta come in to play. I dont know how we are supposed to use the kinetic constraits to find the trans func

Post by **goodwine** » Tue Mar 06, 2007 9:50 am

jgates1 wrote:I am having problems coming up with the equations of motion for problems 3 and 4. It has been a while since dynamics. Could you give a pointer on where to go with these questions so that I can do the rest of each problem?

I guess I would suggest coming to my office hours this afternoon. Without a more specific question I can't answer too much here.

Post by **goodwine** » Tue Mar 06, 2007 10:01 am

mattstorey wrote:can you tell me what im doing wrong on number 4, are we supposed to get an equation of torque in terms of x and its derivative for part a and if so how does theta come in to play. I dont know how we are supposed to use the kinetic constraits to find the trans func

I look at it this way.

The equations we have are

Newton's law for the two pulleys and for the mass (3 equations)
A relationship between the angular velocities of the pulleys and the velocity of the mass (2 equations)

The unknowns are

theta1, theta2 and x
the input torque
the tension in the cable between the two pulleys and the tension between pulley 2 and the mass (these must be different -- otherwise pulley 2 wouldn't move).

We have 5 equations and 6 unknowns, so we should be able to reduce it to one equation with just the input torque and the ouput, x.

drail · Post by **drail** » Tue Mar 06, 2007 9:37 pm

On problem22, I still don't understand the partial fraction expansion. I follow until the third-to-last step.

If you have...
Y(s) = (a s + b)/[(s-1)^2 + 1] + c/(s+1)
...then wouldn't that mean that, in order to undo the expansion, you would have s^s in the numerator? You'd have a*s^2 and c*s^2, correct? If that's the case, then a=c=0 (since the original numerator didn't have an s^2), so all that would be left is b/[(s-1)^2 + 1].

I don't know a lot about partial fraction expansion, but based on the other rules of calculus it seems to me that what I've written above is true. Obviously I'm wrong, but I don't know why or how, and I'd really like to know so if a problem like this shows up again I know how to deal with it. I wouldn't mind being able to correctly work this homework problem, either, but it's a little late notice so I'm mainly concerned with future understanding.

Thanks.

drail · Post by **drail** » Tue Mar 06, 2007 9:38 pm

typo: s^2, not s^s

drail · Post by **drail** » Wed Mar 07, 2007 6:16 am

nevermind. i am dumb.

Euler · Post by **Euler** » Fri Mar 09, 2007 12:38 pm

What is a good book to find more problems involving mechanical dynamics controlled by an electrical circuit? The Laplace transforms are easy once you understand partial fraction expansion, but setting them up is the hard part. I need more practice, either from examples, or a textbook. The class text does not have much on this.

Post by **goodwine** » Fri Mar 09, 2007 1:15 pm

Euler wrote:What is a good book to find more problems involving mechanical dynamics controlled by an electrical circuit? The Laplace transforms are easy once you understand partial fraction expansion, but setting them up is the hard part. I need more practice, either from examples, or a textbook. The class text does not have much on this.

I'm in the process of adding a lot of examples to the notes I'm writing. On the Monday after break, check what's there and it may suffice. Another book would be Feedback Control of Dynamical System, by Frankin and Powell.