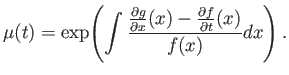AME 30314: Differential Equations, Vibrations and Controls I
Fall 2015
Homework 3
Problem 2
Consider a uniform flexible rope of length ![]() and total mass
and total mass ![]() , as is illustrated on the right in Figure 1. Assume that the length of rope hanging off the end of the table is
, as is illustrated on the right in Figure 1. Assume that the length of rope hanging off the end of the table is ![]() and that the coefficient of friction (both dynamic and static) between the rope and table is
and that the coefficient of friction (both dynamic and static) between the rope and table is ![]() . Determine a differential equation with dependent variable
. Determine a differential equation with dependent variable ![]() and independent variable
and independent variable ![]() that describes the motion of the rope. What are the units for each term in the equation?
that describes the motion of the rope. What are the units for each term in the equation?
Problem 3
Based on Theorem D.1 in the textbook 1, which of the following differential equations are guaranteed to have solutions that exist and are unique?
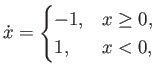
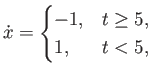
Problem 4
Show that the set of functions
![]() is linearly independent.
is linearly independent.
Problem 5
Show that
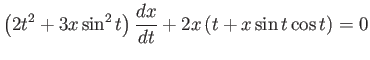
is not exact, but when multiplied by
Problem 6
One special case where it is possible to determine an integrating factor is when it only depends on ![]() . In such a case, the equation:
. In such a case, the equation:
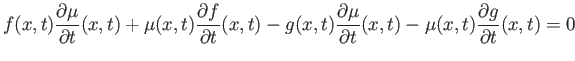
reduces to
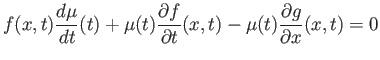
which gives