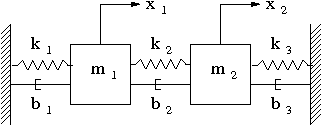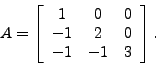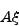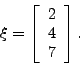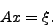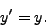- Determine the equations of motion for the following two-mass system. Write them as a system of four first order ordinary differential equation.
- Determine the equations of motion for the following n-mass system. Write the second order differential equation for masses 1, 2, i and n. Also write them as a system of 2n first order ordinary differential equations.
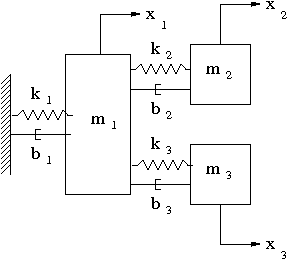
- Determine the equations of motion for the three masses in the following figure. You do not have to convert these to a system of first order equations.
- Consider the matrix
- Compute the eigenvectors and eigenvalues of this matrix by hand. Check your answer using Matlab.
- Pick a vector that is not one of the eigenvectors of A. Plot it and plot A times that vector. Observe that they are not colinear. Plot one of the eigenvectors and then plot A times that eigenvector. Obvserve that they are colinear and that the eigenvector has been scaled by the corresponding eigenvalue.
- Compute the product
- Using elementary row operations, solve the following equation for x
- Determine the general solution to to the scalar differential equation
Homework 1, due January 23, 2008.
Due Wednesday, January 23, 2007.
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Homework 1, due January 23, 2008.
Bill Goodwine, 376 Fitzpatrick
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Re: Matlab
You don't have to print them, but say what matlab gives you since it probably isn't exactly the same, but rather scaled from what you computed. The fact that eigenvectors aren't unique is part of the point of checking.tfurlong wrote:For question four, do we need to print out the checks we do on Matlab to turn in
Bill Goodwine, 376 Fitzpatrick
Return to “AME 30315, Homework 1”
Jump to
- AME 50650, Fall 2018
- ↳ Course Administration
- AME 50652, Spring 2018
- ↳ Course Administration
- ↳ AME 50652, Homework 1
- ↳ AME 50652, Homework 2
- ↳ AME 50652, Homework 3
- ↳ AME 50652, Homework 4
- ↳ AME 50652, Homework 5
- ↳ AME 50652, Homework 6
- ↳ AME 50652, Homework 7
- ↳ AME 50652, Homework 8
- ↳ AME 50652, Homework 9
- ↳ AME 50652, Homework 10
- ↳ AME 50652, Last Homework
- AME 30314, Fall 2017
- ↳ Course Administration
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ Design Project
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Homework 10
- EG 34440, Summer 2017
- ↳ Course Administration
- AME 30315, Spring 2017
- ↳ Course Administration
- ↳ AME 30315, Homework 0
- ↳ AME 30315, Homework 1
- ↳ AME 30315, Homework 2
- ↳ AME 30315, Homework 3
- ↳ AME 30315, Homework 4
- ↳ AME 30315, Homework 5
- ↳ AME 30315, Homework 6
- ↳ AME 30315, Homework 7
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 9
- ↳ AME 30315, Homework 10
- AME 30314, Fall 2016
- ↳ Course Administration
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ Exam 1 Virtual Office Hours
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ Design Project
- ↳ Exam 2, Take 2
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ Project
- ↳ AME 30314, Last Homework
- AME 30314, Fall 2015
- ↳ Course Administration
- ↳ AME 30314, Homework 0
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Exam 2, part deux
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Homework 10
- ↳ AME 30314, Last Homework!
- ↳ Exam 2 Solutions and Final Exam Questions
- AME 90951, Spring 2015
- ↳ Course Administration
- AME 30314, Fall 2014
- ↳ Course Administration
- ↳ AME 30314, Homework 0
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Last Homework
- AME 50650, Spring 2014
- ↳ Course Administration
- ↳ Homeworks
- AME 50652, Spring 2014
- ↳ Course Administration
- ↳ AME 50652, Homework 1
- ↳ AME 50652, Homework 2
- ↳ AME 50652, Homework 3
- ↳ AME 50652, Homework 4
- ↳ AME 50652, Homework 5
- ↳ AME 50652, Homework 6
- ↳ AME 50652, Homework 7
- ↳ AME 50652, Homework 8
- AME 30314, Fall 2013
- ↳ Course Administration
- ↳ AME 30314, Homework 0
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Last Homework
- AME 90951, Spring 2013
- ↳ Course Administration
- ↳ AME 90951 Homeworks
- AME 30314, Fall 2012
- ↳ This Course is on Sakai
- ↳ Homework 0, due Friday August 30, 2013
- AME 30315, Spring 2012
- ↳ Course Administration
- ↳ AME 30315, Homework 0
- ↳ AME 30315, Homework 1
- ↳ AME 30315, Homework 2
- ↳ AME 30315, Homework 3
- ↳ AME 30315, Homework 4
- ↳ AME 30315, Homework 5
- ↳ AME 30315, Homework 6
- ↳ Pendulum Project
- ↳ AME 30315, Homework 7
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 9
- ↳ AME 30315, Homework 10
- ↳ AME 30315, Homework 11
- AME 30314, Fall 2011
- ↳ Course Administration
- ↳ AME 30314, Homework 0
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314: Homework 6
- ↳ AME 30314: Homework 7
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314: Homework X
- ↳ AME 30314, Homework 11
- ↳ AME 30314, Last Homework
- AME 30315, Spring 2011
- ↳ Course Administration
- ↳ AME 30315, Homework 0
- ↳ AME 30315, Homework 1
- ↳ AME 30315, Homework 2
- ↳ AME 30315, Homework 3
- ↳ AME 30315, Homework 4
- ↳ AME 30315, Homework 5
- ↳ AME 30315, Homework 6
- ↳ AME 30315, Homework 7
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 9
- ↳ AME 30315, Homework 10
- ↳ AME 30315, Homework 11
- ↳ AME 30315, Pendulum Control Project
- ↳ AME 30315, Homework 12
- ↳ AME 30315, Homework 13
- AME 30314, Fall 2010
- ↳ Course Administration
- ↳ AME 30314, Homework 0
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ AMe 30314, Homework 9
- ↳ AME 30314, Homework 10
- ↳ AME 30314, Homework 11
- ↳ Virtual Office Hours
- AME 30315, Spring 2010
- ↳ Course Administration
- ↳ AME 30315, Homework 1
- ↳ AME 30315, Homework 2
- ↳ AME 30315, Homework 3
- ↳ AME 30315, Homework 4
- ↳ AME 30315, Homework 5
- ↳ AME 30315, Homework 6
- ↳ AME 30315, Homework 7
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 9
- ↳ AME 30315, Homework 10
- ↳ AME 30315, Last Homework
- ↳ AME 30315, Virtual Office Hours
- AME 20214, Fall 2010
- ↳ Course Administration
- ↳ AME 20214, Homework 0
- ↳ AME 20214, Homework 1
- ↳ AME 20214, Homework 2
- ↳ AME 20214, Homework 3
- ↳ AME 20214, Homework 4
- ↳ AME 20214, Homework 5
- ↳ AME 20214, Homework 6
- ↳ AME 20214, Homework 7
- ↳ AME 20214, Homework 8
- ↳ AME 20214, Final Project
- AME 60652, Spring 2010
- ↳ Course Administration
- ↳ AME 60652, Homework 1
- ↳ AME 60652, Homework 2
- ↳ AME 60652, Homework 3
- ↳ AME 60652, Homework 4
- ↳ AME 60652, Homework 5
- ↳ AMe 60652, Midterm Exam
- ↳ AME 60652, Homework 6
- ↳ AME 60652, Homework 7
- ↳ AME 60652, Homework 8
- ↳ AME 60652, Final Exam
- AME 30314, Fall 2009
- ↳ Course Administration
- ↳ AME 30314, Homework 0
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Homework 10
- AME 30315, Spring 2009
- ↳ Course Administration
- ↳ AME 30315, Homework 1
- ↳ AME 30315, Homework 2
- ↳ AME 30315, Homework 3
- ↳ AME 30315, Homework 4
- ↳ AME 30315, Homework 5
- ↳ AME 30315, Homework 6
- ↳ AME 30315, Homework 7
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 9
- ↳ Pendulum Project
- ↳ AME 30315, Homework 10
- ↳ AME 30315, Homework 11
- ↳ AME 30315, Last Homework
- AME 20214, Fall 2008
- ↳ Course Administration
- ↳ AME 20214, Homework 1
- ↳ AME 20214, Homework 2
- ↳ AME 20214, Homework 3
- ↳ AME 20214, Homework 4
- ↳ AME 20214, Exam I
- ↳ AME 20214, Homework 5
- ↳ AME 20214, Homework 6
- ↳ AME 20214, Homework 7
- ↳ AME 20214, Homework 8
- ↳ AME 20214, Exam II
- ↳ AME 20214, Homework 9
- ↳ AME 20214, Final Exam/Project
- AME 30314, Fall 2008
- ↳ Course Administration
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 3
- ↳ AME 30314 Homework 4
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Homework X
- ↳ AME 30314, Homework 11
- AME 30315, Spring 2008
- ↳ AME 30315, Homework 11
- ↳ AME 30315, Homework 10
- ↳ AME 30315, Homework 9
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 7
- ↳ AME 30315, Homework 6
- ↳ AME 30315, Homework 5
- ↳ AME 30315, Homework 4
- ↳ AME 30315, Homework 3
- ↳ AME 30315, Homework 2
- ↳ AME 30315, Homework 1
- ↳ AME 30315, Homework 0
- ↳ Course Administration
- AME 30314, Fall 2007
- ↳ AME 30314, Homework 10
- ↳ AME 30314, Homework 9
- ↳ AME 30314, Homework 8
- ↳ AME 30314, Homework 7
- ↳ AME 30314, Homework 6
- ↳ AME 30314, Homework 5
- ↳ AME 30314, Homework 4
- ↳ AME 30314, Homework 3
- ↳ AME 30314, Homework 2
- ↳ AME 30314, Homework 1
- ↳ AME 30314, Homework 0
- ↳ Course Administration
- AME 53591, Fall 2007
- ↳ Seminar Reports
- AME 60652, Fall 2007
- ↳ AME 60652, Homework 8
- ↳ AME 60652, Homework 7
- ↳ AME 60652, Homework 6
- ↳ AME 60652 Midterm Exam
- ↳ AME 60652, Homework 5
- ↳ AME 60652, Homework 4
- ↳ AME 60652, Homework 3
- ↳ AME 60652, Homework 2
- ↳ AME 60652, Homework 1
- ↳ Course Administration
- AME 30314, Fall 2006
- ↳ AME 30314 Homework 11
- ↳ AME 30314 Homework 10
- ↳ AME 30314 Homework 9
- ↳ AME 30314 Homework 8
- ↳ AME 30314 Homework 7
- ↳ AME 30314 Homework 6
- ↳ AME 30314 Homework 5
- ↳ AME 30314 Homework 4
- ↳ AME 30314 Homework 3
- ↳ AME 30314 Homework 2
- ↳ AME 30314 Homework 1
- ↳ AME 30314 Homework 0
- ↳ Course Administration
- AME 30315, Spring 2007
- ↳ AME 30315, Homework 10
- ↳ AME 30315, Homework 9
- ↳ AME 30315, Homework 8
- ↳ AME 30315, Homework 7
- ↳ AME 30315 Homework 6
- ↳ AME 30315 Homework 5
- ↳ AME 30315 Homework 4
- ↳ AME 30315 Homework 3
- ↳ AME 30315 Homework 2
- ↳ AME 30315 Homework 1
- ↳ AME 30315 Homework 0
- ↳ Course Administration
- LINKS
- ↳ Computer Resources
- AME 60611, Fall 2006
- ↳ AME 60611 Final Exam
- ↳ AME 60611 Exam 2
- ↳ AME 60611 Homework 6
- ↳ AME 60611 Homework 5
- ↳ AME 60611 Exam 1
- ↳ AME 60611 Homework 4
- ↳ AME 60611 Homework 3
- ↳ AME 60611 Homework 2
- ↳ AME 60611 Homework 1
- ↳ AME 60611 Homework 0
- ↳ Course Administration
- AME 34314, Fall 2005
- ↳ AME 34314 Homework 10
- ↳ AME 34314 Homework 9
- ↳ AME 34314 Homework 8
- ↳ AME 34314 Homework 7
- ↳ AME 34314 Homework 6
- ↳ AME 34314 Homework 5
- ↳ AME 34314 Homework 4
- ↳ AME 34314 Homework 3
- ↳ AME 34314 Homework 2
- ↳ AME 34314 Homework 1
- ↳ AME 34314 Homework 0
- ↳ AME 34314 Course Administration
- AME 302, Spring 2005
- ↳ AME 302 Homework 11
- ↳ AME 301 Homework 10
- ↳ AME 302 Homework 9
- ↳ AME 302 Homework 8
- ↳ AME 302 Homework 7
- ↳ AME 302 Homework 6
- ↳ AME 302 Homework 5
- ↳ AME 302 Homework 4
- ↳ AME 302 Homework 3
- ↳ AME 302 Homework 2
- ↳ AME 302 Homework 1
- ↳ AME 302 Homework 0
- ↳ AME 302 Course Administration
- AME 698, Spring 2005
- ↳ AME 698 Homework 4/Midterm
- ↳ AME 698 Homework 3
- ↳ AME 698 Homework 2
- ↳ AME 698 Homework 1
- ↳ AME 698 Homework 0
- AME 301, Fall 2004
- ↳ AME 301 Homework 10
- ↳ AME 301 Homework 9
- ↳ AME 301 Homework 8
- ↳ AME 301 Homework 7
- ↳ AME 301 Homework 6
- ↳ AME 301 Homework 5
- ↳ AME 301 Homework 4
- ↳ AME 301 Homework 3
- ↳ AME 301 Homework 2
- ↳ AME 301 Homework 1
- ↳ AME 301 Homework 0
- ↳ AME 301 Course Administration
- AME 550, Fall 2004
- ↳ AME 550 Homework 6/Final Exam
- ↳ AME 550 Homework 5/Exam 2
- ↳ AME 550 Homework 4
- ↳ AME 550 Homework 3/Exam 1
- ↳ AME 550 Homework 2
- ↳ AME 550 Homework 1
- ↳ AME 550 Homework 0
- ↳ AME 550 Course Administration