Homework 9, due April 16.

[goodwine]

For all the problems consider the following block diagram.

• 

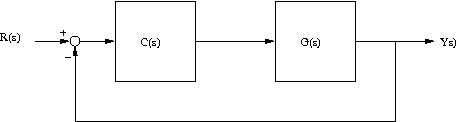
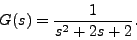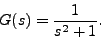1. Let
   • 
   1. Determine a lead compensator, C(s), so that the root locus goes through the point s=-2+2i. What is the gain (k value) corresponding to that point? By considering only the dominant second order poles, predict the rise time, the settling time and the percent overshoot. Use the matlab step() command to verify your predictions. Explain any differences. You may use matlab to verify your computations, but you must do all the computations by hand for full credit.
   2. Repeat the problem, but have the root locus go through the point s=-2+1.75i.
2. Let
   • 
   Determine a lead compensator, C(s), so that the root locus goes through the point s=-2+3i. What is the gain (k value) corresponding to that point? By considering only the dominant second order poles, predict the rise time, the settling time and the percent overshoot. Use the matlab step() command to verify your predictions. Explain any differences.
3. For all three cases above, use the final value theorem to verify the steady state value of the response of the system to a unit step input. It should correspond to the value that the response is converging to in the plot from the matlab step() command.

[rhorning]

Concerning Problem 1, part b, isn't s= -1 + i already a pole? Doesn't the root locus automatically go through the pole, or is that the point?

[goodwine]

Concerning Problem 1, part b, isn't s= -1 + i already a pole? Doesn't the root locus automatically go through the pole, or is that the point?

Ack, sorry. Those numbers are messed up. I'll fix it right now.

[goodwine]

Someone asked me:

For problem 2 on the homework, I get that it's an undamped wave because the poles are on the real axis. If that's the case, should I just describe that instead of finding the rise time, settling time and percent overshoot?

The point of the problem is to design a compensator so that it doesn't do that any more. For the compensated system, what is the rise time, etc.?