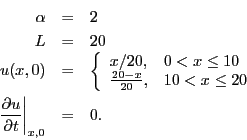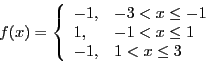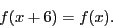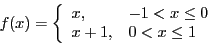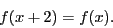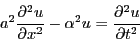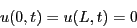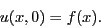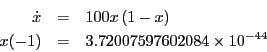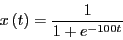Exercises:
- Determine the solution to the wave equation where
Extra credit: make a movie of the solution. - Determine the solution to the wave equation where
Extra credit: make a movie of the solution. - Compute the Fourier series for
- Compute the Fourier series for
- Determine the solution to
- Consider the differential equation
- Show that
- Write a computer program to determine an approximate solution using the 4th order R-K method to this first order differential equation.
- Submit a plot of the approximate solution and the exact solution for this equation for the time interval from t=-1 to t=1. Use trial and error to determine an appropriate step size by comparing your approximate numerical solution to the exact solution for different step sizes and ensure that the magnitude of the maximum error is less than 0.001. Hint the step size has to be pretty small! Be sure to submit your code as well.
- Use the Matlab ode45() function to solve the equation. Submit your code and a plot of the solution and the exact solution. Does Matlab give the correct answer?
- (5 points extra credit) Figure out how to tweak the tolerances in ode45(). Is it possible to get an accurate solution?
- Write a matlab script to implement Euler's method to determine an approximate numerical solution to the above "innocent" equation. An example script using Euler's method to solve the equation
Using this script and Euler's method. Approximately determine how long it would take for the script to run to return an approximate solution that is as accurate as your code from above.
Code: Select all
>> x(1) = -6; >> dt = 0.01; >> t = 0:dt:10; >> for i=2:length(t) x(i)=x(i-1)+sin(t(i-1))*dt; end >> plot(t,x)