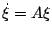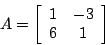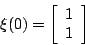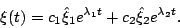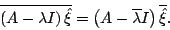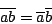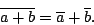- Section 7.6, numbers 2, 4, 7, 8 and 10.
- Solve
- by using one eigenvalue/eigenvector pair and the u(t) and v(t) approach as recommended in class and in the book; and,
- by computing both eigenvalue/eigenvector pairs and directly computing
- To prove that eigenvectors associated with a complex conjugate pair of eigenvalues are also complex conjugates, in class I made use of the fact that if the matrix A is real then
Homework 2, due February 2, 2005.
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Homework 2, due February 2, 2005.
Unless otherwise indicated, all problems are from the course text, Elementary Differential Equations and Boundary Value Problems, by Boyce and DiPrima, 8th Edition.
Last edited by goodwine on Thu Jun 15, 2006 4:24 pm, edited 1 time in total.
-
smanwari
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Get all the way to the sines and cosines (the same answer as part(a)). The point of the problem is to have to actually do this once to see thatsmanwari wrote:For question 2, part b, once we obtain the solution in the form given, do we then have to go through all the algebra and show how this is equal to what we obtained in part a, with the real valued sines and cosines? Or can we just leave it as is, with complex lambdas and eigenvectors?
- the answers are the same; but,
- it's preferable to figure out the u(t) and v(t) approach.
Bill Goodwine, 376 Fitzpatrick
-
NDChevy07
7.6 Problem 7
If we solve the 3x3 Matrix using Matlab, do we need to submit the command window or just write down the values and vectors and then go from there?
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Re: 7.6 Problem 7
Unless there is "programming" involved, i.e., more than one or two commands, you may just write something like "from matlab the eigenvalues and eigenvectors are..."NDChevy07 wrote:If we solve the 3x3 Matrix using Matlab, do we need to submit the command window or just write down the values and vectors and then go from there?
Bill Goodwine, 376 Fitzpatrick
-
7
-
7
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
I suspect that the reason is that the eigenvectors may be arbitrarily scaled. Without seeing exactly how you are doing it in you code, it's hard to say for certain, though.7 wrote:Also, I am getting different values for the eigenvectors when I use Mathematica and the MATLAB code you gave us on 1/21/05. Is there a reason for this?
Bill Goodwine, 376 Fitzpatrick
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
I make a table of (x,y) values (and usually just pick (1,0), (1,1), (0,1), (-1,1) etc.) and then compute the derivative values. The arrow should be anchored at the point you picked and point in the deriction of the derivatives.7 wrote:Is there a trick to darwing direction fields? I am having a difficult time figuring out how to draw these and now I am just frustrated.
Example: \dot \xi = A \xi where
A = [1 2; 3 4]
if you pick \xi = (1,1), then \dot \xi = (3,7). So there will be an arrow starting at the point (1,1) that has a slope of 7/3. Pick another point, compute \xi again and draw the arrow starting at the new point with a slope of y/x where (x,y) are the two derivative terms.
Bill Goodwine, 376 Fitzpatrick