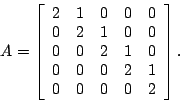- Section 7.8, numbers 7 and 10.
- Find the general solution to
- Find the general solution to
- Find the general solution to
- Find the general solution to
- Find the general solution to
- Write a computer program (in either C or FORTRAN) to determine a numerical approximation to the solution to the equation in the previous problem if the initial conditions are
AME 302 Homework 3, due February 9, 2005.
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
AME 302 Homework 3, due February 9, 2005.
Unless otherwise indicated, all problems are from the course text, Elementary Differential Equations and Boundary Value Problems, by Boyce and DiPrima, 8th Edition.
Last edited by goodwine on Thu Jun 15, 2006 4:24 pm, edited 1 time in total.
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
If there is more than one eigenvector...
A complication regarding computing generalized eigenvectors that I did not anticipate for this homework has arisen. I do not wish to attempt to teach it via this board, so I'm just going to give a hint on how to avoid it.
Whenever you have more than one solution for an eigenvector or generalized eigenvector, i.e., the dimension of the appropriate null space is greater than 1, always pick your eigenvectors to be of the form (1,0,0,0,0)^T, (0,1,0,0,0)^T, etc. This is the case for problems 4, 5 and 6.
This doesn't address the larger issue, but is a way to avoid potential computational complications on this particular homework.
Whenever you have more than one solution for an eigenvector or generalized eigenvector, i.e., the dimension of the appropriate null space is greater than 1, always pick your eigenvectors to be of the form (1,0,0,0,0)^T, (0,1,0,0,0)^T, etc. This is the case for problems 4, 5 and 6.
This doesn't address the larger issue, but is a way to avoid potential computational complications on this particular homework.
Bill Goodwine, 376 Fitzpatrick
-
acrutchf
sketching plots
when the book asks to sketch a plot of x1 v x2, does it mean that x1 is the top row of the solution or that x1 is the solution associated with c1? Either way, is a parametric plot the way to do this?
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Re: sketching plots
x1 = row 1 andacrutchf wrote:when the book asks to sketch a plot of x1 v x2, does it mean that x1 is the top row of the solution or that x1 is the solution associated with c1? Either way, is a parametric plot the way to do this?
x2 = row 2.
To plot solutions, you could use ParametricPlot[] in mathematica or just build up a matrix of solutions in matlab inside a Do or For loop.
Bill Goodwine, 376 Fitzpatrick
-
kdormuth
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Submit whatever you think suffices to compare the analytical and numerical approximate solutions.kdormuth wrote:Hi,
Sorry, I'm still a little confused about #7, with the plotting: I've got a file for time and Xi[0]...Xi[4] and I've loaded all that into MatLab. So, what am I plotting? Xi[0[ vs. t? or Xi[0] vs Xi[1]?
Thanks,
Kristin
Bill Goodwine, 376 Fitzpatrick