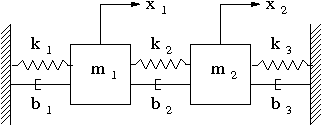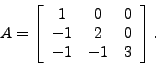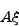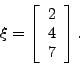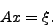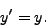Homework 1, due January 24, 2007.

[goodwine]

1. Determine the equations of motion for the following two-mass system. Write them as a system of four first order ordinary differential equation.
   • 
2. Determine the equations of motion for the following n-mass system. Write the second order differential equation for masses 1, 2, i and n. Also write them as a system of 2n first order ordinary differential equations.
   • 
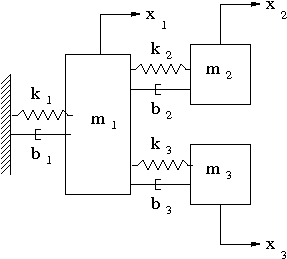
3. Determine the equations of motion for the three masses in the following figure. You do not have to convert these to a system of first order equations.
   • 
4. Consider the matrix
   • 
   1. Compute the eigenvectors and eigenvalues of this matrix by hand. Check your answer using Matlab.
   2. Pick a vector that is not one of the eigenvectors of A. Plot it and plot A times that vector. Observe that they are not colinear. Plot one of the eigenvectors and then plot A times that eigenvector. Obvserve that they are colinear and that the eigenvector has been scaled by the corresponding eigenvalue.
   3. Compute the product
      • 
      where
      • 
      Check this answer using Matlab.
   4. Using elementary row operations, solve the following equation for x
      • 
      Again, check your answer using Matlab.
   Print and submit your work in Matlab along with your calculations done by hand.
5. Determine the general solution to
   • 

[goodwine]

Someone asked me:

I’ve been working on the homework assignment and am having problems with the finding the eigenvectors for part 4.

Below is my work:

A = [ 1 0 0 ]
[ -1 2 0 ]
[ -1 -1 3 ]

I calculated the eigenvalues to be 1, 2, & 3 (since it’s a diagonal matrix). This answer was confirmed by Matlab.

However, to get the eigenvectors, I am having difficulty. I know that you go ahead and subtract lambda*I from matrix A, so for the eigenvalue of 1, we get:

Lambda = 1

[ 0 0 0 ]
[-1 1 0 ]
[-1 -1 2 ]

However, where do I go from here? I calculated the eigenvector of matrix A in Matlab, and could not “work backwards” to where I am right now. I have similar matrices for lambda = 2 and lambda = 3.

I would speculate that your difficulty is because eigenvectors are not unique. All you have to do is solve the three equations you have for the components of the eigenvector. However, the fact that they are not unique is manifested by the row of zeros. You have to assume a value for one of the components and work from there.

[goodwine]

I have been working on question 4 of the homework and came to the part where I have to check my answer to part (a) in MATLAB. I used the MATLAB string [V,D] = eig(A) where A is the Matrix given in the problem. This generates the correct eigenvalues of 1,2, and 3, however it gives me a wierd answer for the eigenvectors... I tried using the MATLAB string for another matrix of which I had the correct eigenvectors and again it gave a messed up answer. Is this the MATLAB string I should be using to calculate the eigenvalues/vectors?

By hand I calculated the eigenvectors to be [2 0 1] , [-1 1 0], [1 0 1] and I believe those to be correct but I cannot seem to verify my calculations with MATLAB. Any help you could offer would be appreciated.

Since eigenvectors are not unique, you may not get the same answer as matlab. I believe that matlab normalizes them. As long as your answer is a scalar multiple of matlab's, then your answers correspond.

Having said that, I think you have a computational error for your eigenvectors.

[goodwine]

Someone asked me:

In Homework #1 Problem 4 Part B, would you like us to graph the vectors by hand or using Matlab.

Either way is fine with me.

[goodwine]

I was trying to confirm my results for the homework in matlab and I was having some trouble using the EIG function to get the eigenvalues and eigenvectors. Is that what students normally use for your class or is there another method which I should use?

That's the one that I'm familiar with.