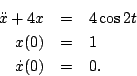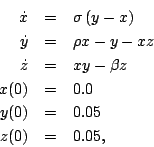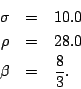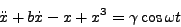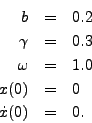Homework 9, due November 8.

[goodwine]

1. Consider
   • 
   This is an example of undamped forced vibrations where the forcing frequency and the natural frequency are the same. Here m=1, k=4, F=4 and the forcing frequency is 2.
   1. Determine the analytical solution.
   2. Convert this second order equation into two first order equations.
   3. Write a computer program that uses the 4th order Runge-Kutta method to compute an approximate solution for the time interval t=0 to t=10. Determine a good time step by comparing the approximate solution to the analytical solution. Submit a plot of the solution.
   4. Plot the solution on the phase plane which is a plot of x(t) on the abscissa and dx/dt on the ordinate. The course text has a discussion of the phase plane as does the course notes that I wrote. Googling "phase plane" gives plenty of descriptive links as well.
2. Consider the famous Lorenz equations
   • 
   where
   • 
   1. Using 4th order Runge-Kutta determine an approximate numerical solution to these equations for the time range t=0 to t=50. Submit a 3D plot of (x,y,z). Be sure to experiment with the time step to ensure that your solution is accurate. The Matlab plot3() function will probably be useful. A quick google search will probably give you an idea of what the plot should look like.
   2. Use Matlab's ode45() to compute an approximate solution and plot the result.
   3. (5 points extra credit) Explain the significance of these equations.
3. Consider
   • 
   with
   • 
   This is another famous equation that has a chaotic solution. Write a computer program to determine an approximate numerical solution using the 4th order Runge-Kutta method to this equation for t=0 to t=100.
   1. Plot x(t) versus t.
   2. Plot the solution on the phase plane.
   3. (5 points extra credit) What is the name of this equation?

[awulz]

Here is what Choice 5 equates to: (Computed in Matlab)

2 Exams worth 18.5914% each
Final worth 42.8172%
Homework worth 20%

Someone please confirm. Thanks
Alex

[dlipp]

That sounds about right.

[mattstorey]

Alternative to Poll

my second choice for the varying weights of tests, homework, and a final is the popular second choice, BUT my 1st choice which i did not see on there would be 3 tests, 16.67% each, then a final worth 30% and homework worth 20%.