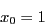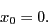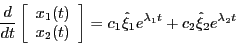- Determine a linear differential equation that is a good approximation of this one near the points
- Near each of those points, find the analytical solution to this linear approximation.
- Near the point
- Near the point
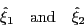 are vectors and x1 and x2 are x(t) and the derivative of x(t) respectively.
are vectors and x1 and x2 are x(t) and the derivative of x(t) respectively.
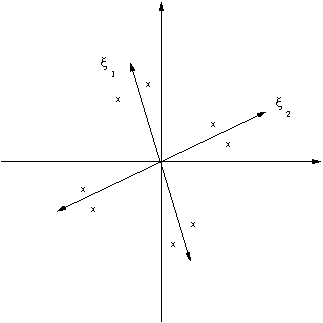
Plot these vectors. Plot (-1) times these vectors. Compare the linear and nonlinear solutions for 8 different initial conditions, one close to and on each side of the vectors plotted, as indicated by the "x"s illustrated in the following figure.
Homework 10, due 5:00pm, December 11.
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Homework 10, due 5:00pm, December 11.
Consider
Bill Goodwine, 376 Fitzpatrick
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Re: Problem 2
If the equation is linear in xdot, then it should not matter what you use; however, if xdot is large, then x will be changing a lot so it may not be likely to hang around x_0. Hence, it's usually a good ideal to make xdot small.aoconno5 wrote:When we are finding the linear approximation to the nonlinear equation, how do we know what value of xdot(0) to use? In the examples you did in the text, you chose xdot(0)=10.2 for one and xdot(0)=0.2 for another and I'm not sure how you picked those values.
Bill Goodwine, 376 Fitzpatrick
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Typo on problem 4
There shouldn't be a d/dt in front of the [x1, x2] vector. That is the solution, not the original differential equation.
Bill Goodwine, 376 Fitzpatrick
-
goodwine
- Site Admin
- Posts: 1596
- Joined: Tue Aug 24, 2004 4:54 pm
- Location: 376 Fitzpatrick
- Contact:
Also on problem 4
Not all of the solutions blow up, but most of them do.
Bill Goodwine, 376 Fitzpatrick