Homework 6

[goodwine]

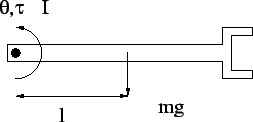
1. Consider the robot arm illustrated in the following figure (the same as we did in class).
   • 
   Write a computer program using 4th order R-K to determine an approximate solution to this system when controlled by PID control (the equations were given in class).
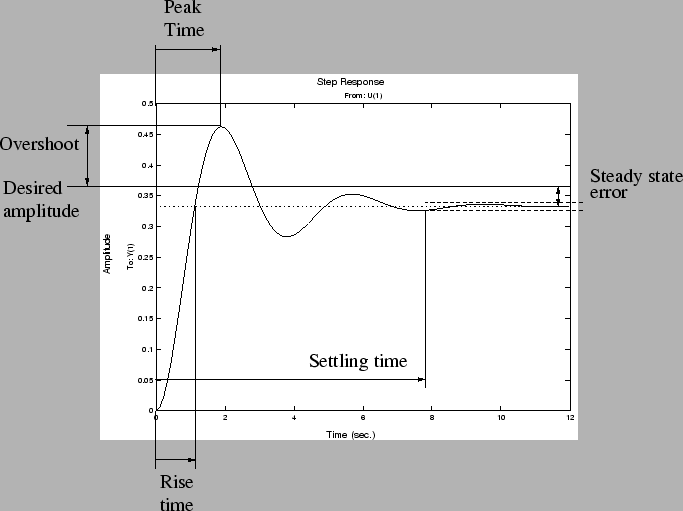
2. Using this program, verify the following "rules of thumb" for PID control using the definitions of ise time, peak time, overshoot, settling time and steady state error from the following figure.
   • 
   1. For proportional control, i.e., kp > 0, kd = 0 and kI=0, the solutions are oscillatory, and increasing kp increases the frequency of oscillation (which decreases the rise time and peak time) but decreases the mean steady state error. The settling time is infinite. Hint pick a starting value of kp=5.
   2. If derivative control is added to the proportional controller, i.e., kp > 0, kd > 0 and kI=0, then
      • for small kd the solutions are decaying oscillations;
      • increasing kd decreases the settling time;
      • increasing kd sufficiently eliminates the oscillatory behavior completely, resulting in an solution which exponentially decays to the final, steady state value;
      • increasing kp decreases the final steady state error;
      • increasing kp decreases the rise time.
      Hint pick a starting value of about kd=0.5.
   3. Adding integral control (PID control)
      • eliminates the steady state error, even for small values of kp,
      • increasing kI generally increases the overshoot and settling time;
      • increasing kp decreases rise time, but may increase overshoot;
      • increasing kd increases damping and stability.
      Hint: pick a starting value of about kI=0.5.