What is Pulse Width Modulation?

Pulse width modulation or PWM is a standard way by which a digital device can generate an analog voltage. This section discusses how you can use the MicroStamp11 to generate a PWM signal that can be interfaced to a simple capacitive circuit and thereby generate an analog voltage.

Let's define a signal as a function that maps time onto some real number. Consider, for instance, a two-terminal electronic device. The voltage over this device at time is denoted as $v(t)$. We can think of $v$ as mapping the time to the voltage $v(t)$.

We say a signal, $v$ is periodic if there exists a positive time $T$ such that $v(t)=v(t+T)$ for all $t \in \Re$. In other words, at any moment, 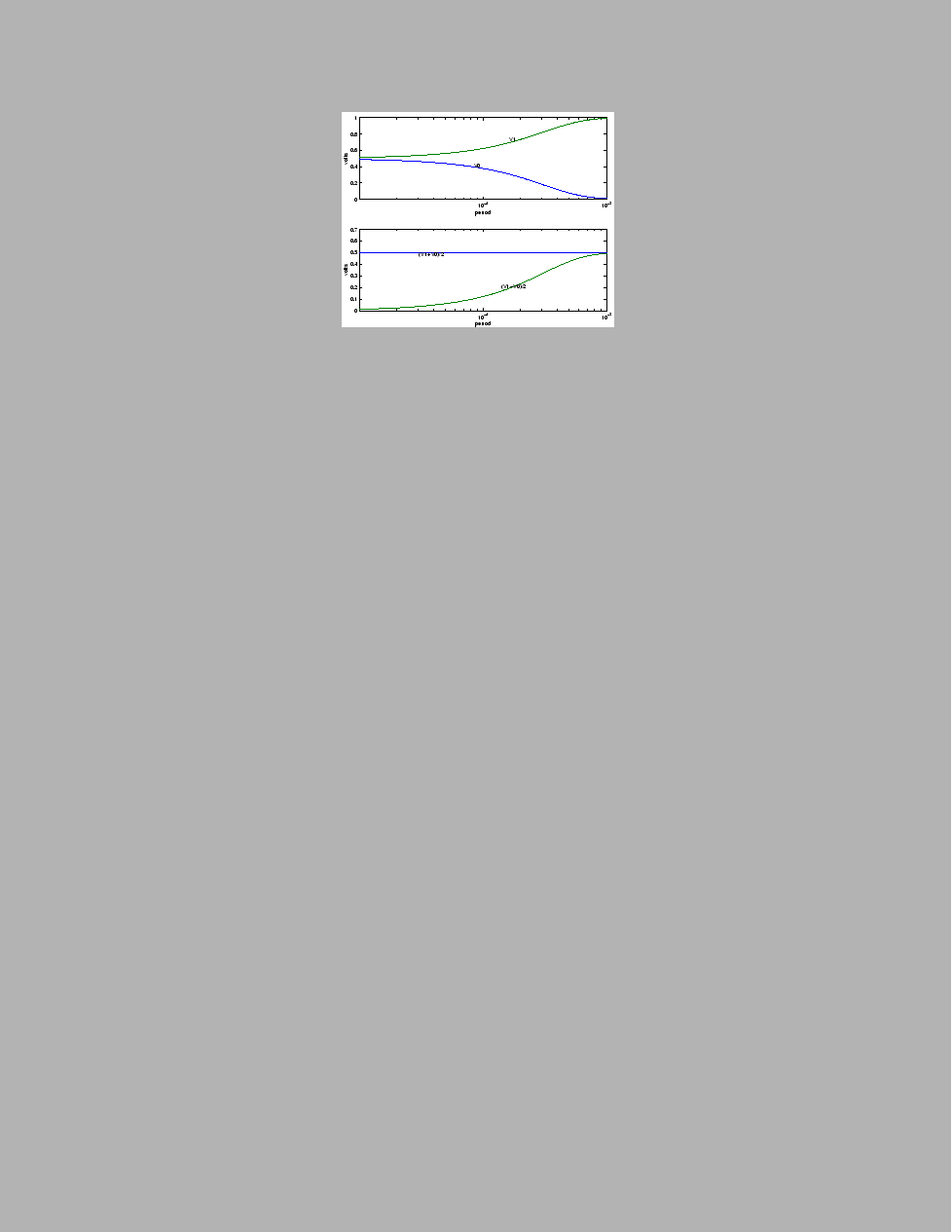, in time, the value of $v$ ($v(t)$) will always be repeated at regular time intervals $T$ in the future. We refer to $T$ as the period of the signal. If $T$ is the smallest such positive number such that $v(t)=v(t+T)$, then we refer to $T$ as the signal's fundamental period. If $T$ is the period of a periodic signal $v$, we often refer to $v$ as being $T$-periodic.

A pulse width modulated signal is a $T$-periodic signal, $v$, where there exists a time such that $0 < T_1 < T$ and such that

$$v(t) = \left\{ \begin{array}{cc} 1 & 0 \leq t < T_1 \\ 0 & T_1 \leq t < T \end{array} \right.$$ (1)

for $t \in [0,T]$. We fer to the ration $T_1/T$ as the duty cycle of the signal. We usually represent the duty cycle as a percentage. Equation 1 defines the values that $v$ takes over a single period, $T$. Since $v$ is $T$-periodic, we know that the pattern characterized in equation 1 will repeat itself at regular intervals of duration $T$. Figure 33 shows a pulse-width modulated signal whose duty cycle is $25 \%$.

Figure 33: Pulse Width Modulated Signal